[zurück]

11.11. Zusammenhang Umkugelradius - Kantenkugelradius

[vor]

Bei einigen regulären Polyedern ist mir ein interessanter Zusammenhang zwischen dem Umkugelradius und dem Kantenkugelradius aufgefallen. Die Formeln enthalten nur ganze Zahlen, die sich zwischen Umkugelradius und Kantenkugelradius nur minimal unterscheiden.
Alle Formeln beziehen sich auf eine Kantenlänge von 1 und sind so formuliert das sie direkt verglichen werden können.

Polyeder	Umkugelradius	Kantenkugelradius
Tetraeder
Hexaeder
Oktaeder
Dodekaeder
Ikosaeder
Abgeschrägtes Hexaeder
Tetraederstumpf
Kuboktaeder
Hexaederstumpf
Oktaederstumpf
Rhombenkuboktaeder   J37 Verlängerte verdrehte Quadratsdoppelkuppel
Großes Rhombenkuboktaeder
Ikosidodekaeder   J34 Fünfecksdoppelrotunde
Dodekaederstumpf
Ikosaederstumpf
Rhombenikosidodekaeder
Großes Rhombenikosidodekaeder
Small ditrigonary icosidodecahedron   Ditrigonal dodecadodecahedron   Rhombihedron
Rhombidodecadodecahedron   Icosidodecadodecahedron   Rhombicosahedron
Small Snub Icosicosidodecahedron
Great dodecicosahedron   Great ditrigonal dodecicosidodecahedron   Great icosicosidodecahedron
Small dodecicosidodecahedron   Small rhombidodecahedron
Small stellated truncated dodecahedron
Nonconvex great rhombicuboctahedron   Great cubicuboctahedron   Great rhombihexahedron

Alle Formeln enthalten nur ganze Zalen, das hat eine gewisse Ästhetik. Bei einigen Formeln beträgt der Nenner 2 und bei einigen beträgt er 4. Das läßt sich aber durch einen gemeinsamen Hauptnenner ändern. Das demonstriere ich am Beispiel des Hexaederstumpfs.

Führen wir eine Polyederspezifische Konstante p ein dann läßt sich der Umkugelradius r_u und der Kantenkugelradius r_k wie folgt ausdrücken.

Lösen wir r_u nach p auf.

Jetzt setzen wir p in r_k ein.

So erhalten wir eine allgemeingültige Beziehung zwischen dem Umkugelradius r_u und dem Kantenkugelradius r_k.

        bzw.        

Diese Beziehung gilt für alle platonischen und archimedischen Körper und wahrscheinlich auch für alle anderen Polyeder, die eine Um- und Kantenkugel besitzen.

Das gilt auch im 2D Bereich für regelmäßige Vielecke (Kantenlänge = 1).

Vieleck	Umkreisradius	Inkreisradius
Dreieck
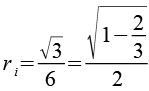Viereck
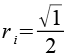Fünfeck
Sechseck
Achteck
Zehneck
Zwölfeck
Sechzehneck

Für den Umkreisradius r_u und der Inkreisradius r_i erhalten wir

Die Formel läßt sich auch für beliebige Nenner erweitern, so lassen sich einige Formeln einfacher schreiben.

Vieleck	Umkreisradius	Inkreisradius
Dreieck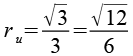
Fünfeck

Für den Umkreisradius r_u und der Inkreisradius r_i erhalten wir dann

So erhalten wir analog zu den Polyedern eine allgemeingültige Beziehung zwischen dem Umkreisradius r_u und dem Inkreisradius r_i der regelmäßigen Vielecke.

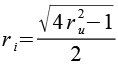
Das läßt sich natürlich auch viel einfacher über den Pythagoras herleiten, z.B. am Fünfeck (Kantenlänge = a).

Und bei den Polyedern am Beispiel des Dodekaeders.

Der Inkugelradius eines Polygons im Polyeder (er berührt die Mitte des Polygons) läßt sich leicht über den Umkugelradius des Polyeders r_u berechnen. Dazu benötigt man nur noch den Umkreisradius des Polygons und kann den Inkugelradius des Polygons mit dem Pythagoras berechnen.

Polygon	Umkreisradius Polygon	Inkugelradius Polyeder
Dreieck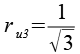
Viereck
Fünfeck
Sechseck
Achteck
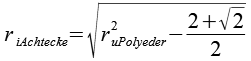Zehneck

[zurück]

[Inhaltsverzeichnis]

[vor]