11.9. Small dodecicosidodecahedron, Small rhombidodecahedron, Small stellated truncated dodecahedron
|
[zurück] | 11.9. Small dodecicosidodecahedron, Small rhombidodecahedron, Small stellated truncated dodecahedron |
[vor] | |
Vom Rhombenikosidodekaeder leiten sich der Small dodecicosidodecahedron, der Small rhombidodecahedron und der Small stellated truncated dodecahedron ab. Alle Polyeder haben die gleichen Eckpunkte bzw. Koordinaten.
Small dodecicosidodecahedron
 |
 |
| Isometrie | Dimetrie |
| Name | Small dodecicosidodecahedron |
| Anzahl Ecken | 60 |
| Anzahl Kanten | 120 |
| Anzahl Flächen | 20 Dreiecke 12 Fünfecke 12 Zehnecke |
| Kantenlänge | 1 |
| Umkugelradius |  |
| Kantenkugelradius |  |
| Inkugelradius (Dreiecke) |  |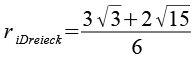
| Inkugelradius (Fünfecke) |  |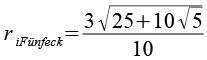
| Inkugelradius (Zehnecke) |  |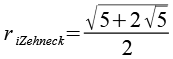
nur Zehnecke
Der Small dodecicosidodecahedron mit seiner Umkugel.
Der Small dodecicosidodecahedron mit seiner Kantenkugel.
Der Small dodecicosidodecahedron mit seiner Inkugel (Dreiecke). Die Inkugel (violett) ist zur Veranschaulichung so dimensioniert das sie gerade so die entsprechende Fläche durchdringt.
Der Small dodecicosidodecahedron mit seiner Inkugel (Fünfecke).
Der Small dodecicosidodecahedron mit seiner Inkugel (Zehnecke).
Small rhombidodecahedron
 |
 |
| Isometrie | Dimetrie |
| Name | Small rhombidodecahedron |
| Anzahl Ecken | 60 |
| Anzahl Kanten | 120 |
| Anzahl Flächen | 30 Vierecke 12 Zehnecke |
| Kantenlänge | 1 |
| Umkugelradius | |
| Kantenkugelradius | |
| Inkugelradius (Vierecke) |  |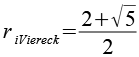
| Inkugelradius (Zehnecke) | |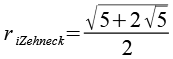
Der Small rhombidodecahedron mit seiner Umkugel.
Der Small rhombidodecahedron mit seiner Kantenkugel.
Der Small rhombidodecahedron mit seiner Inkugel (Vierecke). Die Inkugel (violett) ist zur Veranschaulichung so dimensioniert das sie gerade so die entsprechende Fläche durchdringt.
Small stellated truncated dodecahedron
 |
 |
| Isometrie | Dimetrie |
| Name | Small stellated truncated dodecahedron |
| Anzahl Ecken | 60 |
| Anzahl Kanten | 90 |
| Anzahl Flächen | 12 Fünfecke 12 Dekagramme |
| Kantenlänge | 1 |
| Umkugelradius |  |
| Kantenkugelradius |  |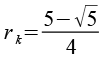
| Inkugelradius (Fünfecke) |  |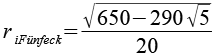
| Inkugelradius (Dekagramme) |  |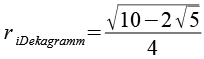
nur Fünfecke
nur Dekagramme
Der Small stellated truncated dodecahedron mit seiner Umkugel.
Der Small stellated truncated dodecahedron mit seiner Kantenkugel.
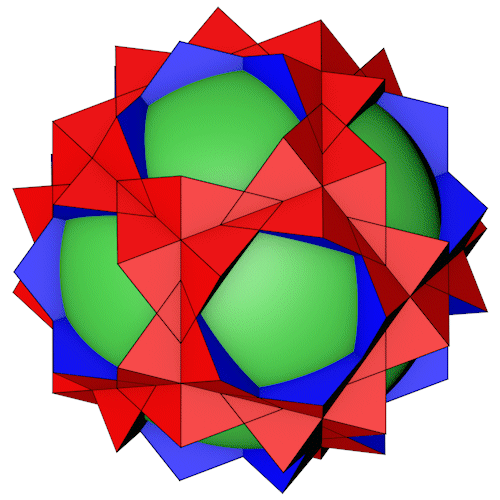
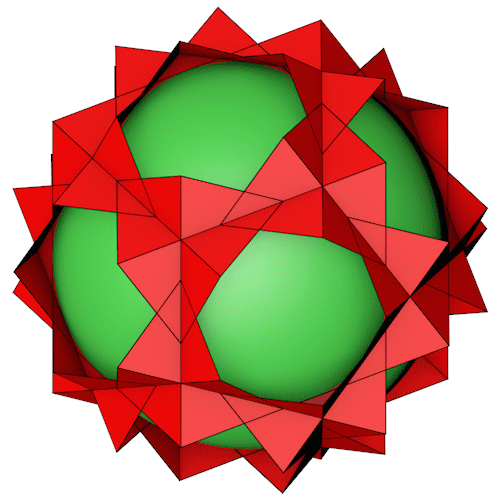
Der Small stellated truncated dodecahedron mit seiner Inkugel (Dekagramme). Die Inkugel (grün) ist zur Veranschaulichung so dimensioniert das sie gerade so die entsprechende Fläche durchdringt.
Der Small stellated truncated dodecahedron mit seiner Inkugel (Fünfecke). Es werden nur 2 der 12 Fünfecke dargestellt.
6 Prismen
Die 60 Punkte lassen sich zu 6 Prismen mit Pentagrammen als Grundfläche verbinden. Einmal wurden die 6 Pismen unterschiedlich gefärbt und einmal die Grundflächen (Pentagramme) rot und die Seitenflächen (Vierecke) blau.
 |
 |
 |
 |
| Isometrie | Dimetrie |
| Anzahl Ecken | 60 |
| Anzahl Kanten | 0 |
| Anzahl Flächen | 60 Vierecke 12 Pentagramme |
Da die Pentagramme aus den Zehnecken erzeugt werden sind zwei chirale Varianten möglich.
 |
 |
| Variante A | Variante B |
Beide Varianten lassen sich in einem Bild zusammenfassen.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |