11.8. Great dodecicosahedron, Great ditrigonal dodecicosidodecahedron, Great icosicosidodecahedron
|
[zurück] | 11.8. Great dodecicosahedron, Great ditrigonal dodecicosidodecahedron, Great icosicosidodecahedron |
[vor] | |
Vom Dodekaederstumpf leiten sich der Great dodecicosahedron, der Great ditrigonal dodecicosidodecahedron und der Great icosicosidodecahedron ab. Alle Polyeder haben die gleichen Eckpunkte bzw. Koordinaten.
Great dodecicosahedron
 |
 |
| Isometrie | Dimetrie |
| Name | Great dodecicosahedron |
| Anzahl Ecken | 60 |
| Anzahl Kanten | 120 |
| Anzahl Flächen | 20 Sechsecke 12 Dekagramme |
| Kantenlänge | 1 |
| Umkugelradius |  |
| Kantenkugelradius |  |
| Inkugelradius (Sechsecke) |  |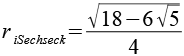
| Inkugelradius (Dekagramme) |  |
nur Sechsecke
nur Dekagramme
Der Great dodecicosahedron mit seiner Umkugel.
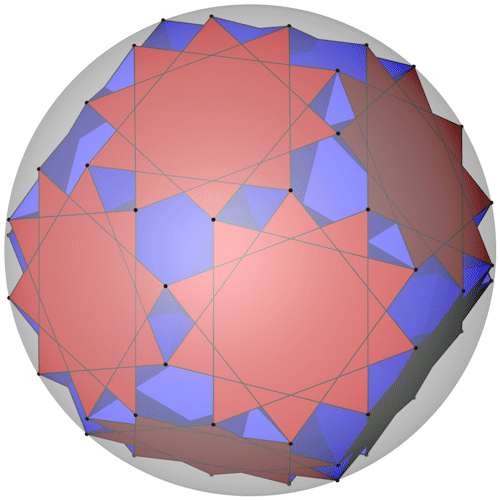
Der Great dodecicosahedron mit seiner Kantenkugel.
 |
 |
| nur Sechsecke |
Der Great dodecicosahedron mit seiner Inkugel (Dekagramme). Die Inkugel (grün) ist zur Veranschaulichung so dimensioniert das sie gerade so die entsprechende Fläche durchdringt.
Der Great dodecicosahedron mit seiner Inkugel (Sechsecke). Die Inkugel (grün) ist zur Veranschaulichung so dimensioniert das sie gerade so die entsprechende Fläche durchdringt. Die vorderen Sechsecke wurden gelöscht.
Great ditrigonal dodecicosidodecahedron
 |
 |
| Isometrie | Dimetrie |
| Name | Great ditrigonal dodecicosidodecahedron |
| Anzahl Ecken | 60 |
| Anzahl Kanten | 120 |
| Anzahl Flächen | 20 Dreiecke 12 Fünfecke 12 Dekagramme |
| Kantenlänge | 1 |
| Umkugelradius | |
| Kantenkugelradius | |
| Inkugelradius (Dreiecke) |  |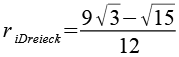
| Inkugelradius (Fünfecke) |  |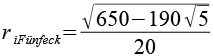
| Inkugelradius (Dekagramme) | |
nur Dreiecke (blau) und Fünfecke (grün)
nur Dreiecke
Der Great ditrigonal dodecicosidodecahedron mit seiner Umkugel.
Der Great ditrigonal dodecicosidodecahedron mit seiner Kantenkugel.
 |
 |
| nur Dreiecke (blau) und Fünfecke (grün) |
Der Great ditrigonal dodecicosidodecahedron mit seiner Inkugel (Dreiecke). Die Inkugel (grün) ist zur Veranschaulichung so dimensioniert das sie gerade so die entsprechende Fläche durchdringt.
Der Great ditrigonal dodecicosidodecahedron mit seiner Inkugel (Fünfecke). Die Inkugel (grün) ist zur Veranschaulichung so dimensioniert das sie gerade so die entsprechende Fläche durchdringt.
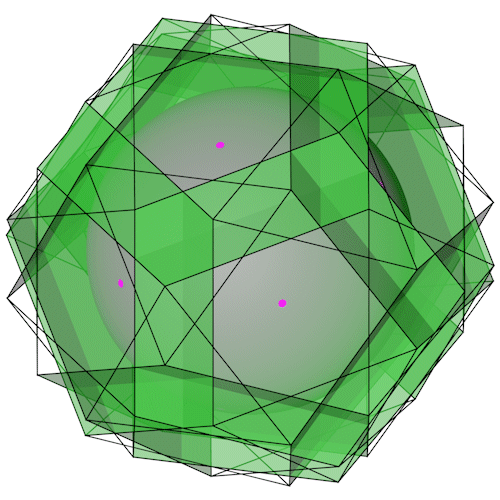
Great icosicosidodecahedron
 |
 |
| Isometrie | Dimetrie |
| Name | Great icosicosidodecahedron |
| Anzahl Ecken | 60 |
| Anzahl Kanten | 120 |
| Anzahl Flächen | 20 Dreiecke 12 Fünfecke 20 Sechsecke |
| Kantenlänge | 1 |
| Umkugelradius | |
| Kantenkugelradius | |
| Inkugelradius (Dreiecke) | |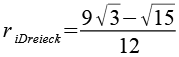
| Inkugelradius (Fünfecke) | |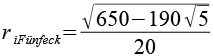
| Inkugelradius (Sechsecke) | |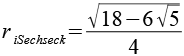
nur Dreiecke (blau) und Sechsecke (rot)
nur Fünfecke (grün) und Sechsecke (rot)
Der Great icosicosidodecahedron mit seiner Umkugel.
Der Great icosicosidodecahedron mit seiner Kantenkugel.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |