11.7. Small Snub Icosicosidodecahedron
|
[zurück] | 11.7. Small Snub Icosicosidodecahedron |
[vor] | |
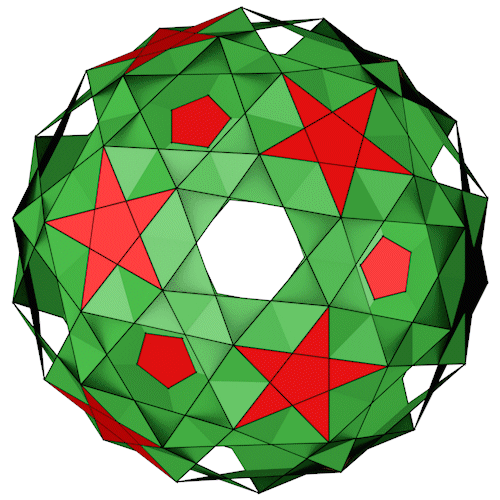
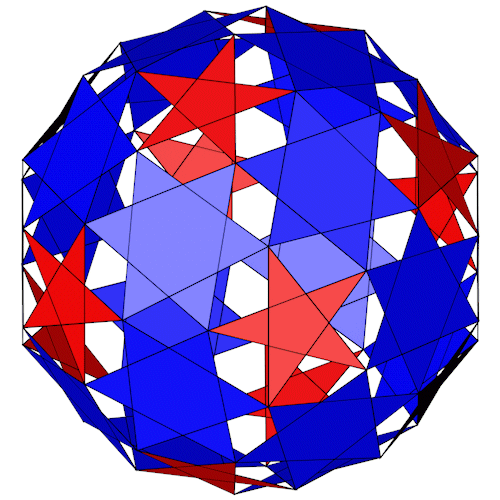
Der Small Snub Icosicosidodecahedron besteht aus 100 gleichseitigen Dreiecken und 12 Pentagrammen. 60 Dreiecke bilden paarweise 30 "Near Miss" Hexagramme die ich teilweise separat gefärbt habe (blau und grün).
 |
 |
 |
 |
| Isometrie | Dimetrie |
| Name | Small Snub Icosicosidodecahedron |
| Anzahl Ecken | 60 |
| Anzahl Kanten | 180 |
| Anzahl Flächen | 100 Dreiecke 12 Pentagramme |
| Kantenlänge | 1 |
| Umkugelradius |  |
| Kantenkugelradius |  |
| Inkugelradius (Dreieck) |  |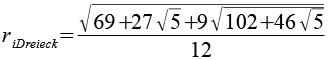
| Inkugelradius (Pentagramm) |  |
 |
 |
 |
 |
Der Small Snub Icosicosidodecahedron mit seiner Umkugel.
Der Small Snub Icosicosidodecahedron mit seiner Kantenkugel.
Der Small Snub Icosicosidodecahedron mit seiner Inkugel (Dreiecke). Die Inkugeln sind zur Veranschaulichung so dimensioniert das sie gerade so die entsprechende Fläche durchdringen.
Der Small Snub Icosicosidodecahedron mit seiner Inkugel (Pentagramm).
Die Koordinaten der Eckpunkte des Small Snub Icosicosidodecahedron lassen sich aus folgenden Beziehungen herleiten, daraus ergibt sich eine Kantenlänge von 4. Phi ist der goldene Schnitt.
Mit
und
Aus
werden die 3 geraden Permutationen gebildet, durch Variation der Vorzeichen ergeben sich die ersten 12 Punkte.
Aus
werden die 3 geraden Permutationen gebildet, durch Variation der Vorzeichen ergeben sich die nächsten 24 Punkte.
Aus
werden die 3 geraden Permutationen gebildet, durch Variation der Vorzeichen ergeben sich die letzten 24 Punkte.
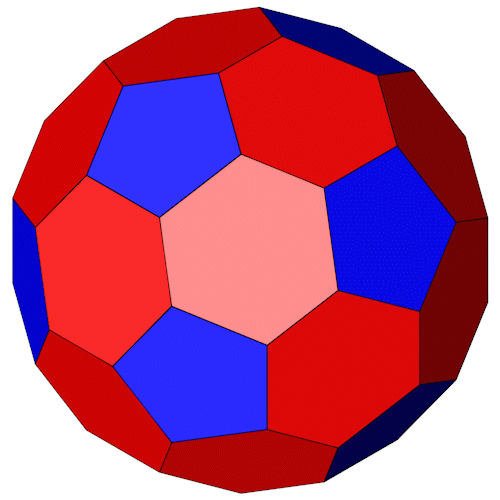
Der Small Snub Icosicosidodecahedron wird von einem "Near Miss" Ikosaederstumpf umhüllt. Die Fünfecke sind regulär, die Sechsecke haben zwei unterschiedliche Seiten.
 |
 |
| Hüllkurve | Ikosaederstumpf |
Wenn die Kantenlänge des Small Snub Icosicosidodecahedron a = 1 ist (Diagonale des Fünfecks) dann sind die Kanten der Hüllkurve wie folgt definiert (phi ist der goldene Schnitt).
Der Small Snub Icosicosidodecahedron mit seiner Hüllkurve.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |