[zurück]

11.6. Rhombidodecadodecahedron, Icosidodecadodecahedron, Rhombicosahedron

[vor]

Neben dem Rhombidodecadodecahedron lassen sich aus diesen Punkten auch der Icosidodecadodecahedron und der Rhombicosahedron erzeugen.

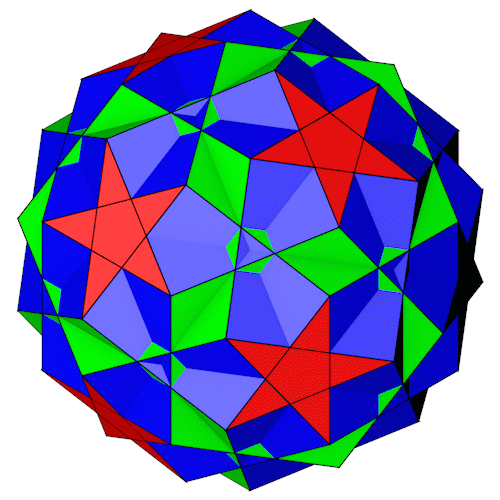
Rhombidodecadodecahedron

Isometrie	Dimetrie

Name	Rhombidodecadodecahedron
Anzahl Ecken	60
Anzahl Kanten	120
Anzahl Flächen	30 Vierecke 12 Fünfecke 12 Pentagramme
Kantenlänge	1
Umkugelradius
Kantenkugelradius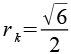
Inkugelradius (Vierecke)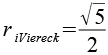
Inkugelradius (Fünfecke)
Inkugelradius (Pentagramme)

Der Rhombidodecadodecahedron mit seiner Umkugel.

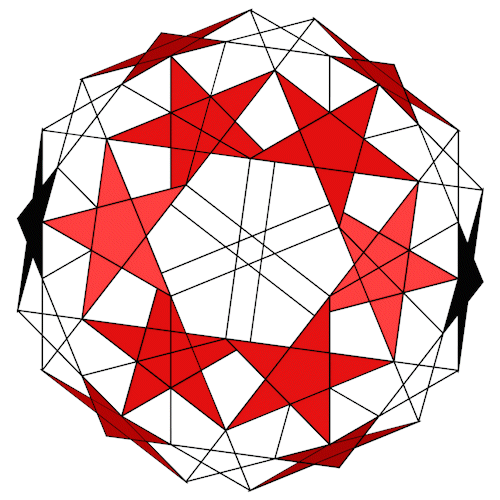
Der Rhombidodecadodecahedron mit seiner Kantenkugel.

Der Rhombidodecadodecahedron mit seiner Kantenkugel. Es werden nur die Pentagramme dargstellt.

Der Rhombidodecadodecahedron mit seiner Kantenkugel. Es werden nur die Vierecke dargestellt.

Der Rhombidodecadodecahedron mit seiner Kantenkugel. Es werden nur die Fünfecke dargestellt.

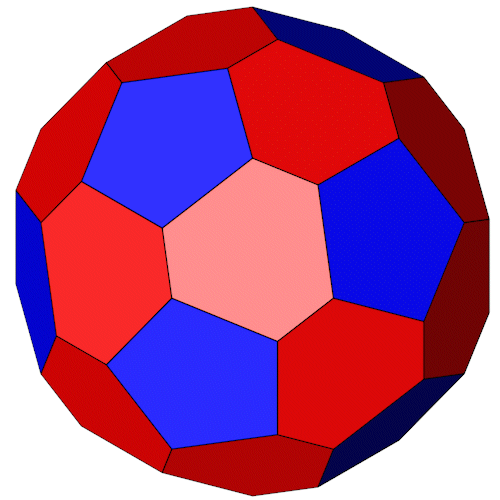
Der Rhombidodecadodecahedron wird von einem "Near Miss" Ikosaederstumpf umhüllt. Die Fünfecke sind regulär, die Sechsecke haben zwei unterschiedliche Seiten.

Hüllkurve	Ikosaederstumpf

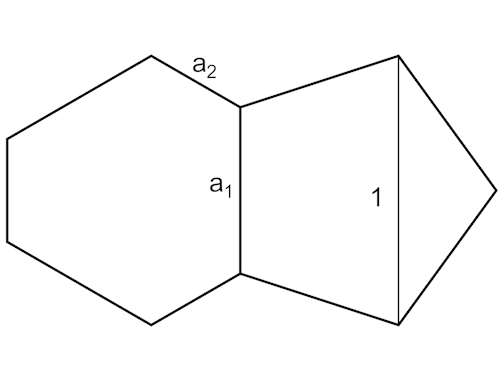
Wenn die Kantenlänge des Rhombidodecadodecahedrons a = 1 ist (Diagonale des Fünfecks) dann sind die Kanten der Hüllkurve wie folgt definiert (phi ist der goldene Schnitt).

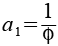
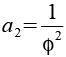
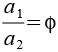
Icosidodecadodecahedron

Name	Icosidodecadodecahedron
Anzahl Ecken	60
Anzahl Kanten	120
Anzahl Flächen	12 Fünfecke 20 Sechsecke 12 Pentagramme
Kantenlänge	1
Umkugelradius
Kantenkugelradius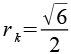
Inkugelradius (Fünfecke)
Inkugelradius (Sechsecke)
Inkugelradius (Pentagramme)

Rhombicosahedron

Name	Rhombicosahedron
Anzahl Ecken	60
Anzahl Kanten	120
Anzahl Flächen	30 Vierecke 20 Sechsecke
Kantenlänge	1
Umkugelradius
Kantenkugelradius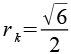
Inkugelradius (Vierecke)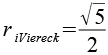
Inkugelradius (Sechsecke)

[zurück]

[Inhaltsverzeichnis]

[vor]