11.5. Truncated great dodecahedron
|
[zurück] | 11.5. Truncated great dodecahedron |
[vor] | |
 |
 |
| Isometrie | Dimetrie |
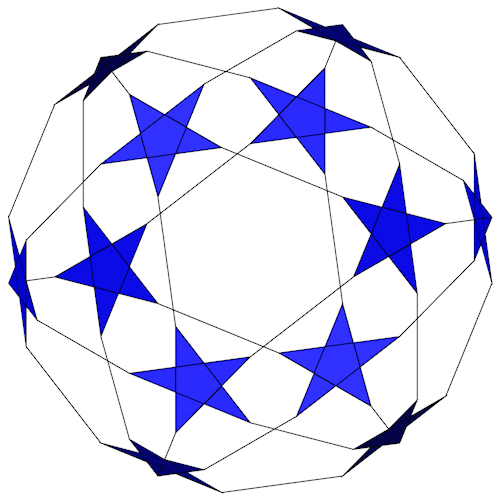
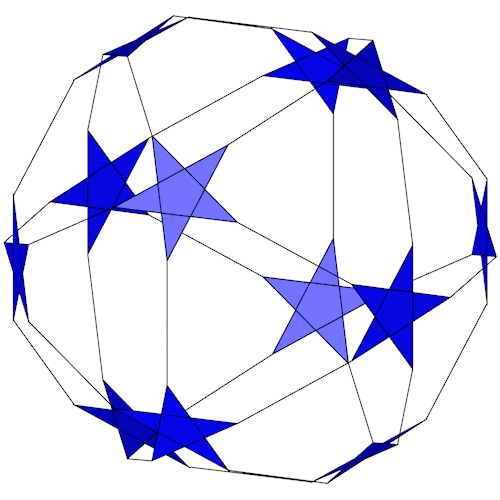
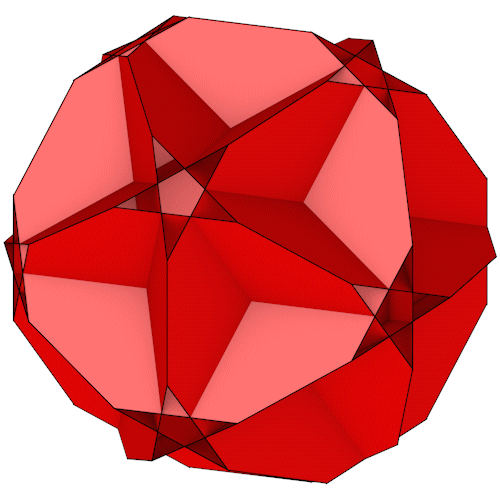
| Name | Truncated great dodecahedron |
| Anzahl Ecken | 60 |
| Anzahl Kanten | 90 |
| Anzahl Flächen | 12 Zehnecke 12 Pentagramme |
| Umkugelradius |  |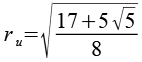
| Kantenkugelradius |  |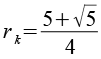
| Inkugelradius (Pentagramm) |  |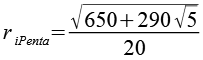
 |
 |
 |
 |
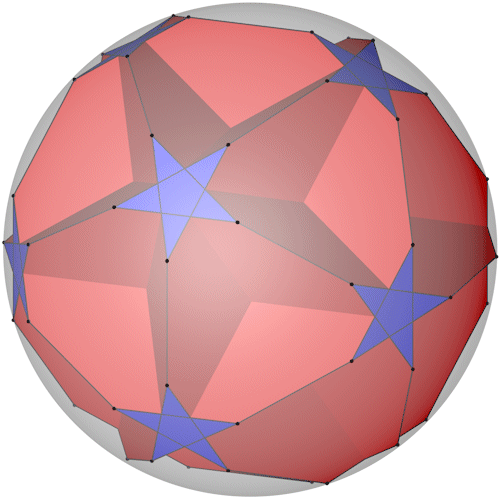
Der Truncated great dodecahedron mit seiner Umkugel.
Der Truncated great dodecahedron mit seiner Kantenkugel.
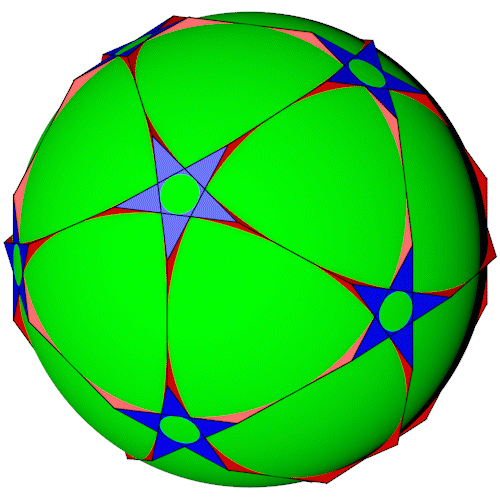
Der Truncated great dodecahedron mit seiner Inkugel (Pentagramme).
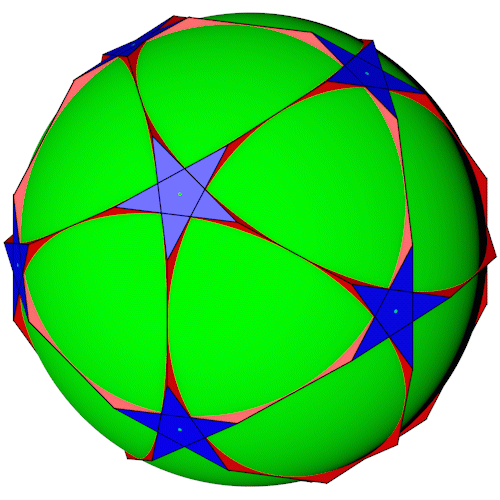
Die Koordinaten der Eckpunkte des Truncated great dodecahedron lassen sich aus folgenden Beziehungen herleiten. Phi ist der goldene Schnitt.
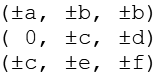
Mit
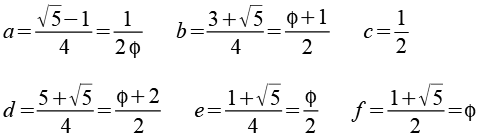
Aus
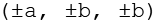
werden die 3 geraden Permutationen gebildet, durch Variation der Vorzeichen ergeben sich die ersten 24 Punkte.
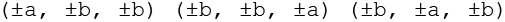
Aus
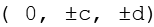
werden die 3 geraden Permutationen gebildet, durch Variation der Vorzeichen ergeben sich die nächsten 12 Punkte.
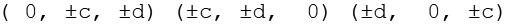
Aus
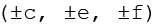
werden die 3 geraden Permutationen gebildet, durch Variation der Vorzeichen ergeben sich die letzten 24 Punkte.
|
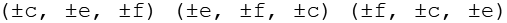
[zurück] | [Inhaltsverzeichnis] | [vor] | |