11.4. Small ditrigonary icosidodecahedron, Ditrigonal dodecadodecahedron und Rhombihedron
|
[zurück] | 11.4. Small ditrigonary icosidodecahedron, Ditrigonal dodecadodecahedron und Rhombihedron |
[vor] | |
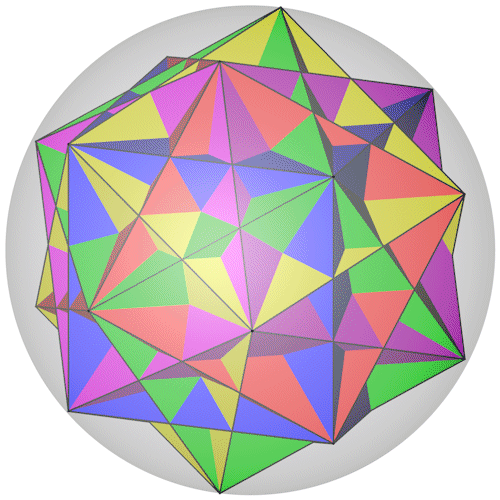
Small ditrigonary icosidodecahedron
 |
 |
| Isometrie | Dimetrie |
| Name | Small ditrigonary icosidodecahedron |
| Anzahl Ecken | 20 |
| Anzahl Kanten | 60 |
| Anzahl Flächen | 20 Dreiecke 12 Pentagramme |
| Umkugelradius |  |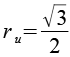
 |
 |
 |
 |
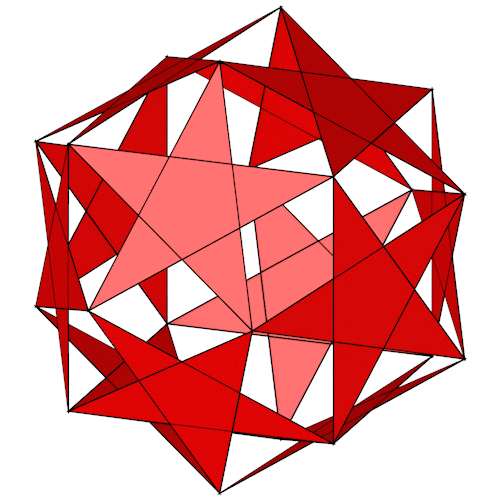
Der Small ditrigonary icosidodecahedron mit seiner Umkugel.
Die Koordinaten der Eckpunkte des Small ditrigonary icosidodecahedron lassen sich aus folgenden Beziehungen herleiten. Phi ist der goldene Schnitt.
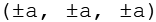
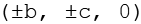
Mit
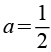
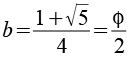
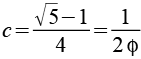
Aus
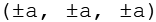
ergeben sich durch Variation der Vorzeichen die ersten 8 Punkte. Aus
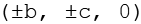
werden die 3 geraden Permutationen gebildet, durch Variation der Vorzeichen ergeben sich die letzen 12 Punkte.
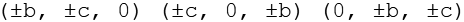
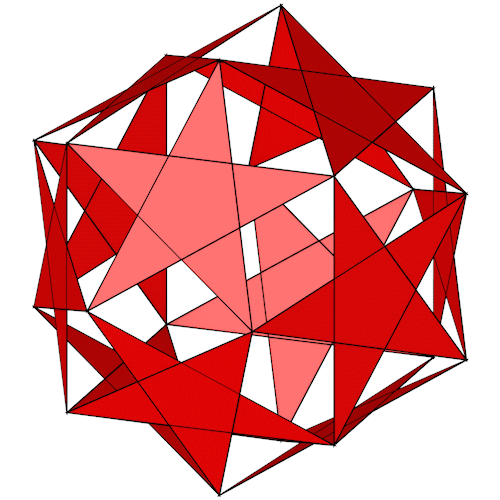
Ditrigonal Dodecadodecahedron
Der Ditrigonal Dodecadodecahedron läßt sich aus den Eckpunkten des Small ditrigonary icosidodecahedron herleiten.
 |
 |
| Isometrie | Dimetrie |
| Name | |
| Anzahl Ecken | 20 |
| Anzahl Kanten | 60 |
| Anzahl Flächen | 12 Fünfecke 12 Pentagramme |
| Umkugelradius | |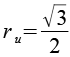
 |
 |
 |
 |
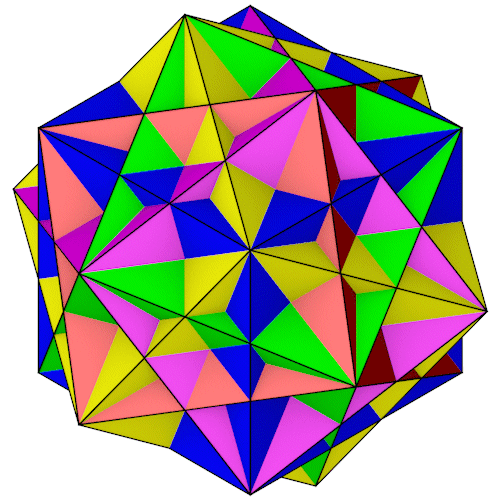
Rhombihedron
Der Rhombihedron läßt sich aus den Eckpunkten des Small ditrigonary icosidodecahedron herleiten. Er besteht aus 5 Würfeln.
 |
 |
 |
 |
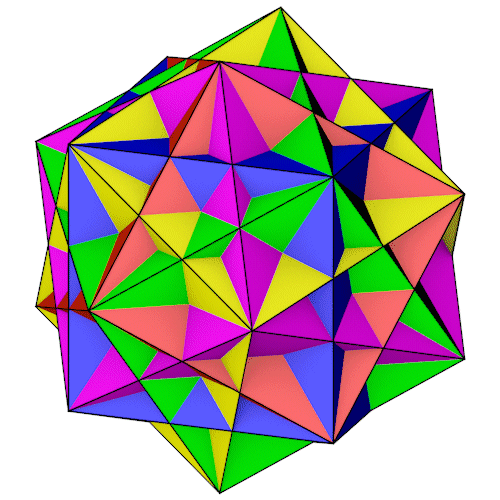| Isometrie | Dimetrie |
| Name | Rhombihedron |
| Anzahl Ecken | 20 |
| Anzahl Kanten | 60 |
| Anzahl Flächen | 30 Vierecke |
| Umkugelradius | |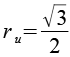
| Inkugelradius |  |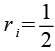
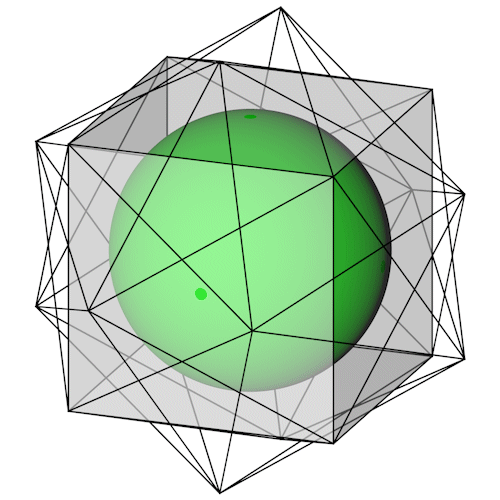
Der Rhombihedron mit seiner Umkugel.
Der Rhombihedron mit seiner Inkugel, dargestellt ist nur ein Würfel.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |