| [zurück] | 3.8. Ikosidodekaeder |
[vor] |
 |
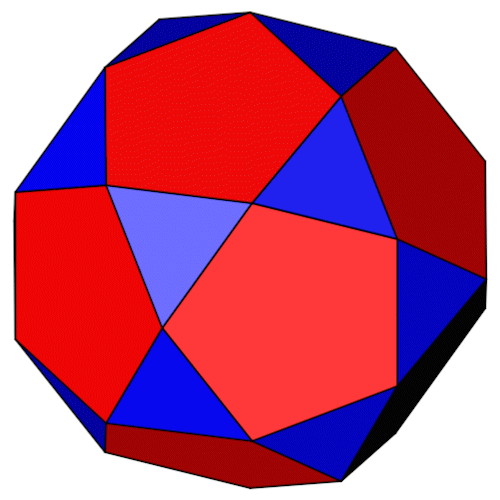 |
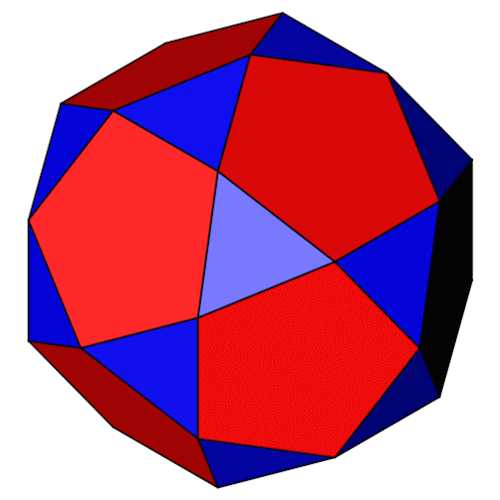
| Isometrie | Dimetrie |
| Name | Ikosidodekaeder Icosidodecahedron |
| Anzahl Ecken | 30 |
| Anzahl Kanten | 60 |
| Anzahl Flächen | 20 Dreiecke 12 Fünfecke |
| Kantenlänge | a |
| Umkugelradius | 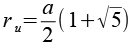 |
| Kantenkugelradius | 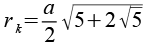 |
| Inkugelradius (Dreiecke) | 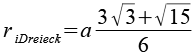 |
| Inkugelradius (Fünfecke) | 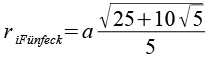 |
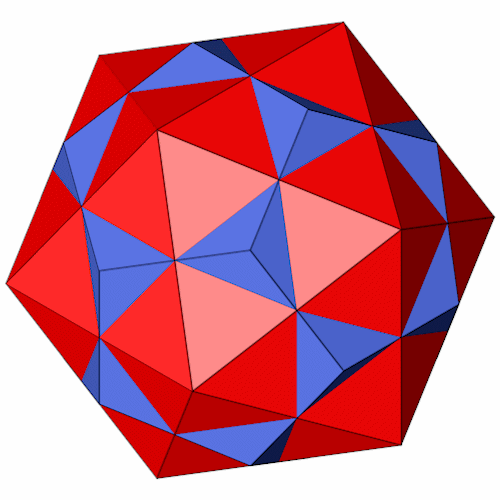
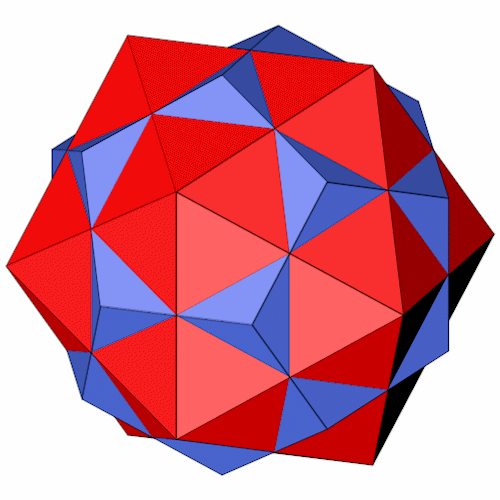
Der Ikosidodekaeder läßt sich aus der Schnittmenge eines Dodekaeders und eines Ikosaeders bilden.
 |
 |
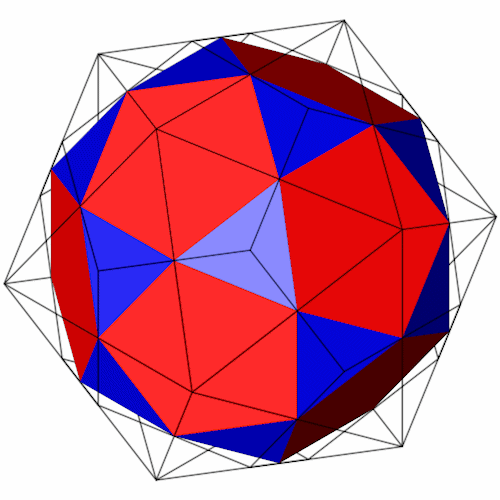 |
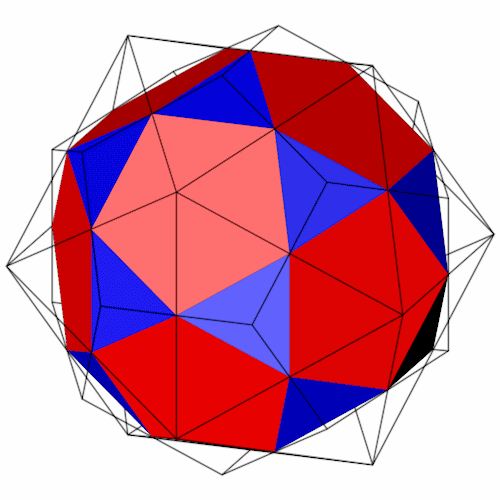 |
Die Seitenansichten.

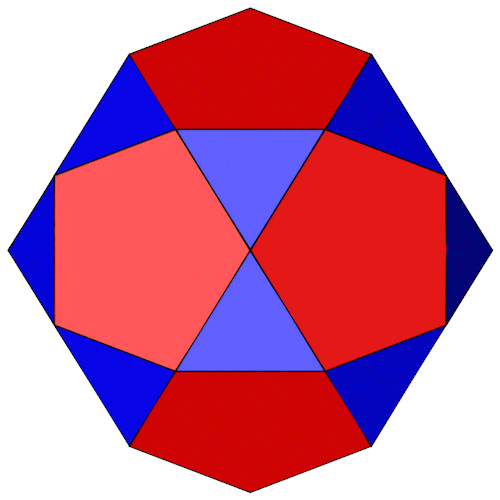
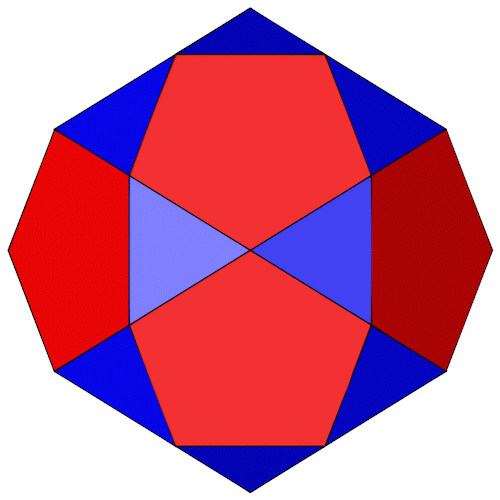
Den Ikosidodekaeder kann man in zwei Fünfecksrotunden (Johnson Körper J6) zerschneiden.
Der Ikosidodekaeder mit seiner Umkugel.

Der Ikosidodekaeder mit seiner Kantenkugel.

Die Koordinaten der Eckpunkte des Ikosidodekaeders lassen sich aus folgender Beziehung herleiten. Phi ist dabei der goldene Schnitt.
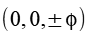
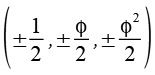
Daraus werden die 3 geraden Permutationen gebildet.
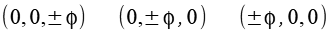
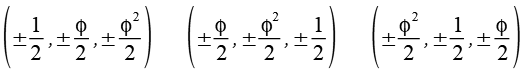
Durch Variation der Vorzeichen ergeben sich 30 Punkte, für die Kantenlänge gilt a = 1.
Vom Ikosidodekaeder bzw. seinen Koordinaten lassen sich weitere Polyeder ableiten.
Small Icosihemidodecahedron
 |
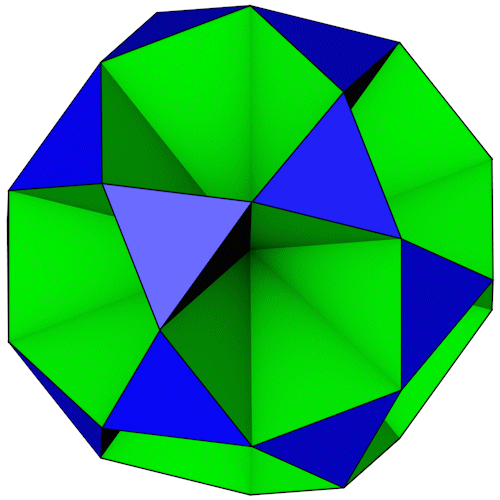 |
| Name | |
| Anzahl Ecken | 30 |
| Anzahl Kanten | 60 |
| Anzahl Flächen | 20 Dreiecke 6 Zehnecke |
 |
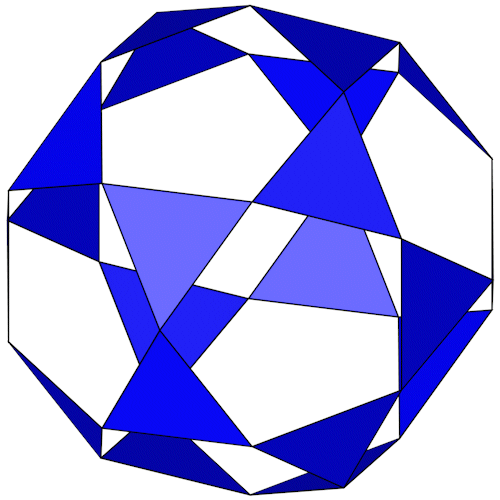 |
 |
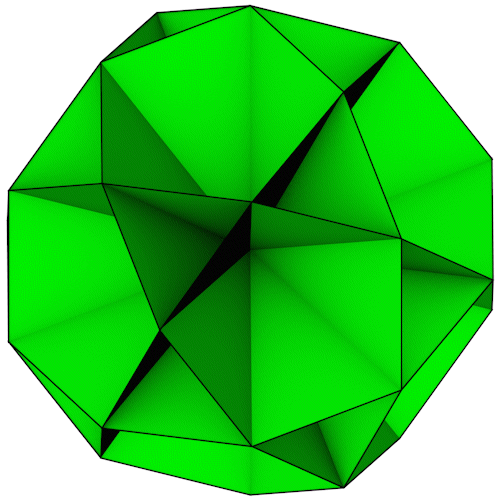 |
Small Dodecahemidodecahedron
 |
 |
| Name | |
| Anzahl Ecken | 30 |
| Anzahl Kanten | 60 |
| Anzahl Flächen | 12 Fünfecke 6 Zehnecke |
 |
 |
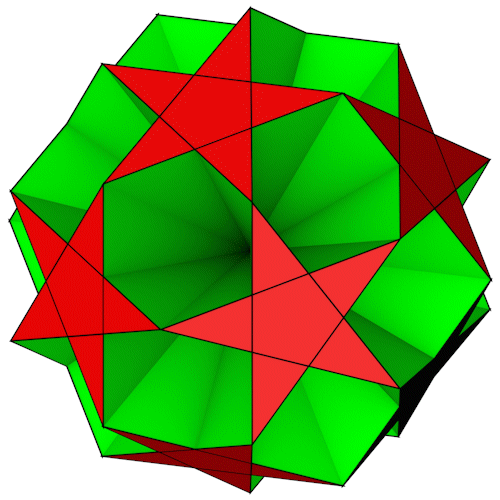
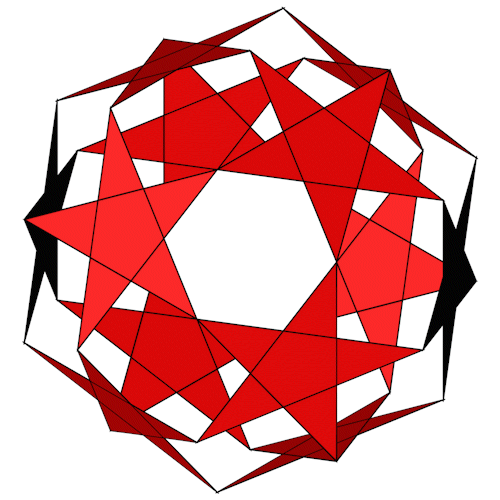
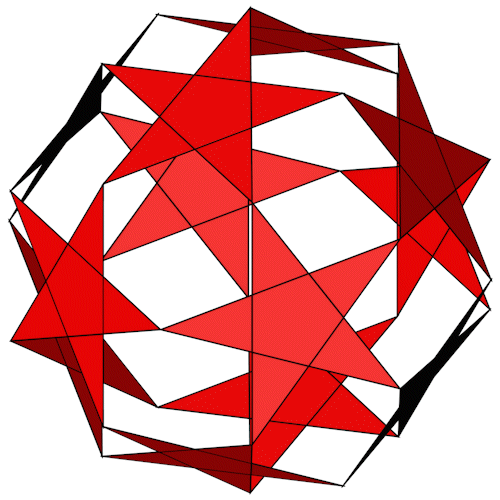
Small Dodecahemicosahedron
 |
 |
| Name | |
| Anzahl Ecken | 30 |
| Anzahl Kanten | 60 |
| Anzahl Flächen | 10 Sechsecke 12 Pentagramme |
 |
 |
 |
 |
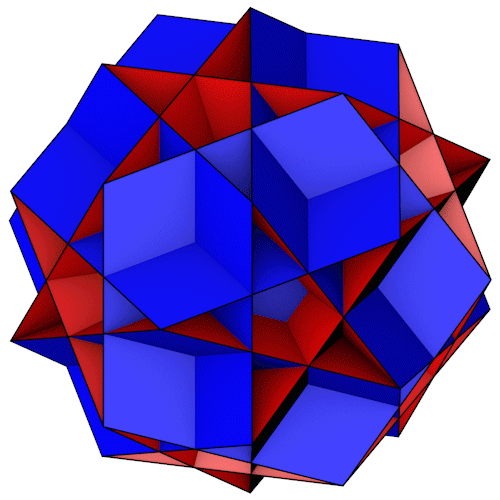
Great-Dodecahemicosahedron
 |
 |
| Name | |
| Anzahl Ecken | 30 |
| Anzahl Kanten | 60 |
| Anzahl Flächen | 12 Fünfecke 10 Sechsecke |
 |
 |
Dodecadodecahedron
 |
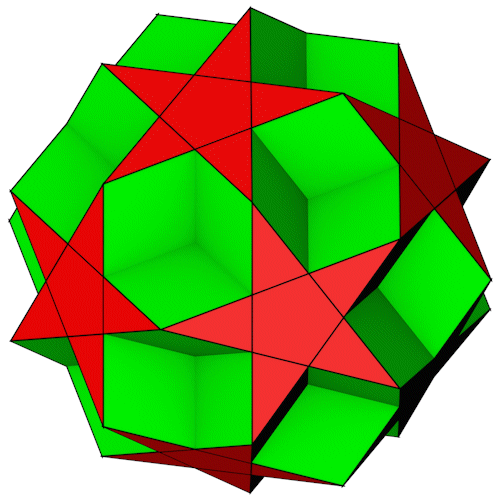 |
| Name | |
| Anzahl Ecken | 30 |
| Anzahl Kanten | 60 |
| Anzahl Flächen | 12 Fünfecke 12 Pentagramme |
| [zurück] | [Inhaltsverzeichnis] | [vor] |