2.1. Tetraeder
|
[zurück] | 2.1. Tetraeder |
[vor] | |
 |
 |
| Isometrie | Dimetrie |
| Name | Tetraeder |
| Schläfli-Symbol {p,q} | {3,3} |
| Anzahl Ecken | 4 |
| Anzahl Kanten | 6 |
| Anzahl Flächen | 4 gleichseitige Dreiecke |
| Kantenlänge | a |
| Volumen |  |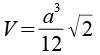
| Oberflächeninhalt |  |
| Inkugelradius |  |
| Kantenkugelradius |  |
| Umkreiskugelradius |  |
Der Tetraeder mit seiner Umkugel.
Der Tetraeder mit seiner Kantenkugel.
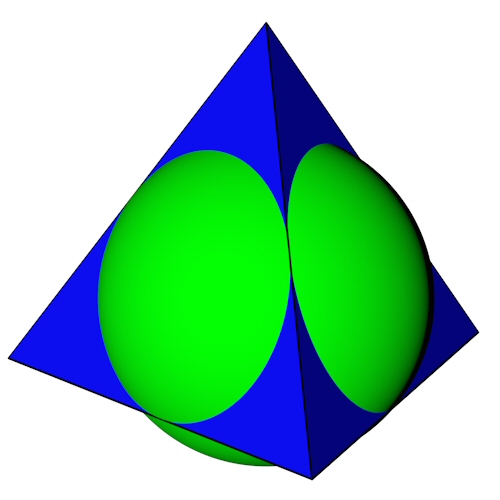
Der Tetraeder mit seiner Innenkugel.
Die Eckpunkte sind wie folgt definiert.
Die Kantenlänge beträgt.
 |
 |
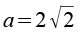
| Isometrie | Dimetrie |
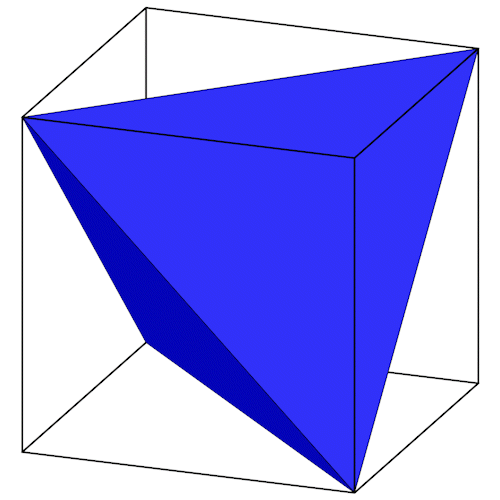
Der Tetraeder wird von einem Würfel umschrieben.
 |
 |
| Isometrie | Dimetrie |
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |