3.6. Großes Rhombenkuboktaeder
|
[zurück] | 3.6. Großes Rhombenkuboktaeder |
[vor] | |
 |
 |
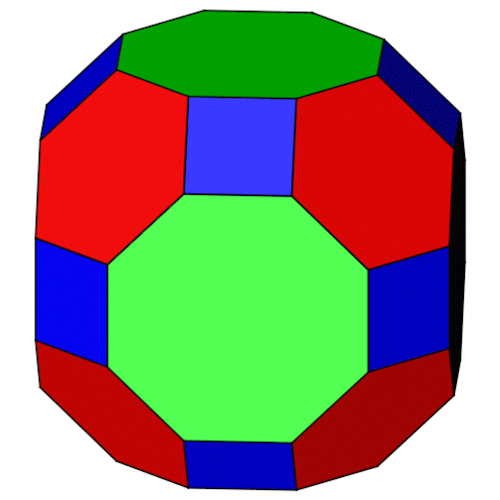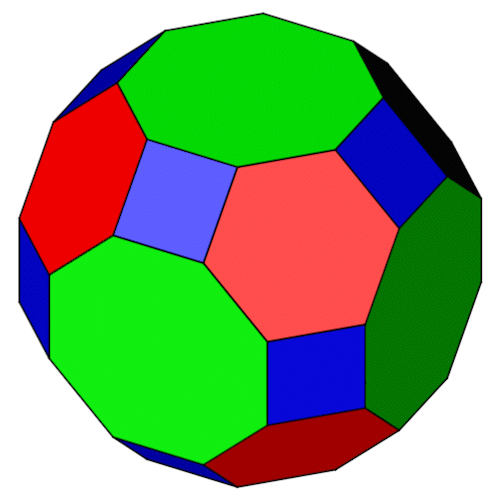
| Isometrie | Dimetrie |
| Name | Großes Rhombenkuboktaeder Kuboktaederstumpf Truncated cuboctahedron |
| Anzahl Ecken | 48 |
| Anzahl Kanten | 72 |
| Anzahl Flächen | 12 Vierecke 8 Sechsecke 6 Achtecke |
| Kantenlänge | a |
| Umkugelradius |  |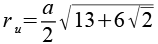
| Kantenkugelradius |  |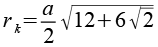
| Inkugelradius (Vierecke) |  |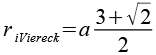
| Inkugelradius (Sechsecke) |  |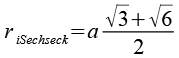
| Inkugelradius (Achtecke) |  |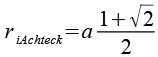
Die drei Seitenansichten.
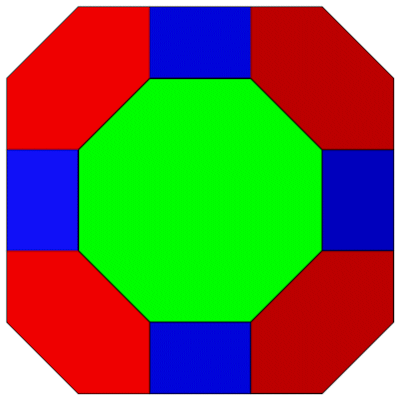
Das Große Rhombenkuboktaeder mit seiner Umkugel.
Das Große Rhombenkuboktaeder mit seiner Kantenkugel.
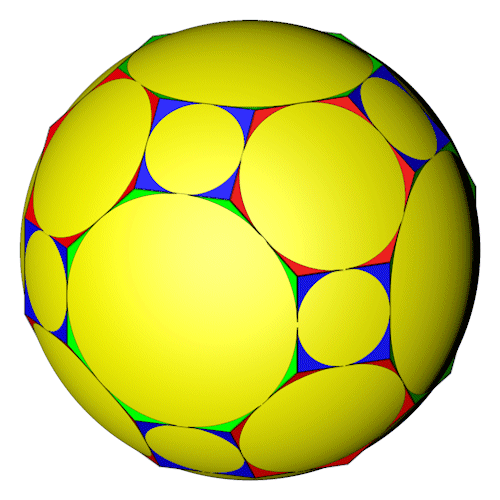
Das Große Rhombenkuboktaeder (blau) mit seinem dualen Körper, dem Hexakisoktaeder (rot). Der duale Körper bildet auf den Flächen des Großen Rhombenkuboktaeders gleichmäßige Pyramiden.
Die Koordinaten der Eckpunkte des Großen Rhombenkuboktaeders lassen sich aus folgender Beziehung herleiten.
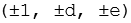
Mit
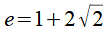
Daraus werden alle 6 Permutationen gebildet.
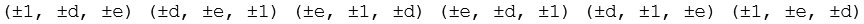
Durch Variation der Vorzeichen ergeben sich 48 Punkte, für die Kantenlänge gilt a = 2.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |