| [zurück] | 3.1. Tetraederstumpf |
[vor] |
 |
 |
| Isometrie | Dimetrie |
| Name | Tetraederstumpf Truncated tetrahedron |
| Anzahl Ecken | 12 |
| Anzahl Kanten | 18 |
| Anzahl Flächen | 4 Dreiecke 4 Sechsecke |
| Kantenlänge | a |
| Umkugelradius |  |
| Kantenkugelradius |  |
| Inkugelradius (Dreiecke) |  |
| Inkugelradius (Sechsecke) |  |
Die drei Seitenansichten.



Der Tetraederstumpf entsteht durch Abstumpfen der Ecken eines Tetraeders.
 |
 |
Der Tetraederstumpf läßt sich in einen Würfel einpassen, alle Punkte des Tetraederstumpfs liegen auf der Oberfläche des Würfels. Drei Kanten der Sechsecke liegen auf den Seitenflächen des Würfels.

In den Tetraederstumpf läßt sich ein Tetraeder einpassen dessen Eckpunkte die Mittelpunkte der Sechsecke berühren.
 |
 |
Der Tetraederstumpf mit seiner Umkugel.

Der Tetraederstumpf mit seiner Kantenkugel.

Für den Tetraederstumpf gibt es, wie bei allen archimedischen Körpern, keine Inkugel aber zwei Kugeln die jeweils die Dreiecke und die Sechsecke in der Mitte berühren.
 |
 |
Der Tetraederstumpf (blau) mit seinem dualen Körper, dem Triakistetraeder (rot). Der duale Körper bildet auf den Flächen des Tetraederstumpfs gleichmäßige Pyramiden.

Herleitung der Koordinaten.
Die Koordinaten der Eckpunkte des Tetraederstumpfs lassen aus folgender Beziehung herleiten.

Zuerst werden die 8 Varianten gebildet, die sich aus den verschiedenen Vorzeichen ergeben.

Von den 8 Koordinaten werden die 4 ausgewählt die eine ungerade Zahl an Pluszeichen (1 oder 3) haben.

Von diesen 4 Koordinaten werden die ersten drei Permutationen gebildet und wir erhalten die 12 Koordinaten des Tetraederstumpfs.

Die Koordinaten des Tetraeders, der in den Tetraederstumpf eingepasst werden kann, läßt sich ähnlich herleiten.

Zuerst werden die 8 Varianten gebildet, die sich aus den verschiedenen Vorzeichen ergeben. Ausgewählt werden dann die Koordinaten mit ungerader Anzahl Minuszeichen (1 oder 3).
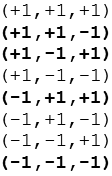
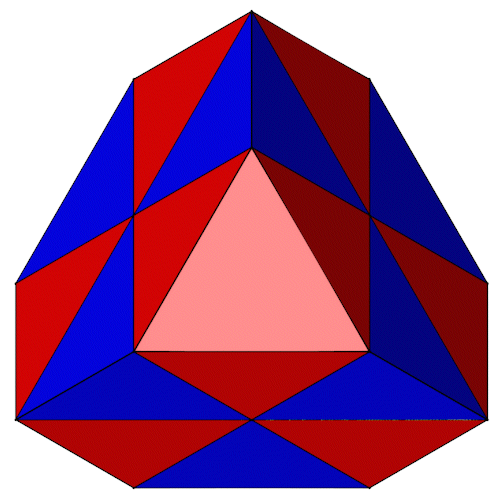
Der Tetraederstumpf läßt sich auch aus 4 Oktaedern (rot) und 6 Tetraedern (blau) zusammensetzen.
 |
 |
 |
 |
 |
 |
| [zurück] | [Inhaltsverzeichnis] | [vor] |