| [zurück] | 2.3. Oktaeder |
[vor] |
 |
 |
| Isometrie | Dimetrie |
| Name | Oktaeder |
| Schläfli-Symbol {p,q} | {3,4} |
| Anzahl Ecken | 6 |
| Anzahl Kanten | 12 |
| Anzahl Flächen | 8 gleichseitige Dreiecke |
| Kantenlänge | a |
| Volumen |  |
| Oberflächeninhalt | 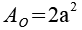
|
| Inkugelradius | 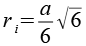 |
| Kantenkugelradius | 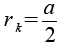 |
| Umkreiskugelradius |  |
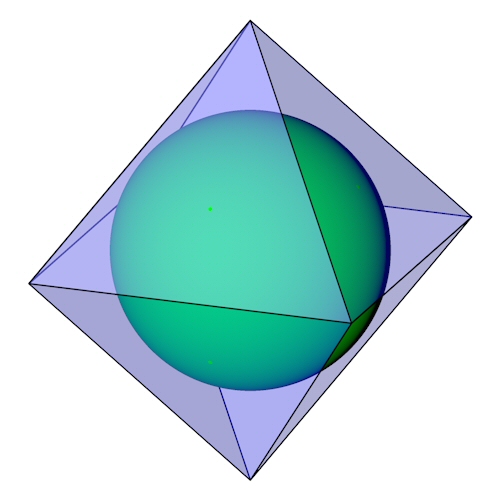
Der Oktaeder mit seiner Umkugel.

Der Oktaeder mit seiner Kantenkugel.

Der Oktaeder mit seiner Innenkugel.
Die Koordinaten der Eckpunkte des Oktaeders lassen sich aus folgender Beziehung herleiten. Phi ist der goldene Schnitt.
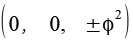
Daraus werden die geraden Permutationen gebildet.
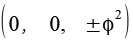
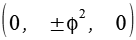
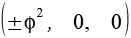
Durch Variation der Vorzeichen entstehen die 6 Punkte. Für die Kantenlänge a gilt.
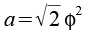
Vom Oktaeder leitet sich der Tetrahemihexahedron ab.
 |
 |
| Anzahl Ecken | 6 |
| Anzahl Flächen | 4 Dreiecke 3 Vierecke |
| [zurück] | [Inhaltsverzeichnis] | [vor] |