3.12. Großes Rhombenikosidodekaeder
|
[zurück] | 3.12. Großes Rhombenikosidodekaeder |
[vor] | |
 |
 |
| Isometrie | Dimetrie |
| Name | Großes Rhombenikosidodekaeder Ikosidodekaederstumpf Truncated icosidodecahedron |
| Anzahl Ecken | 120 |
| Anzahl Kanten | 180 |
| Anzahl Flächen | 30 Vierecke 20 Sechsecke 12 Zehnecke |
| Kantenlänge | a |
| Umkugelradius |  |
| Kantenkugelradius |  |
| Inkugelradius (Vierecke) |  |
| Inkugelradius (Sechsecke) |  |
| Inkugelradius (Zehnecke) |  |
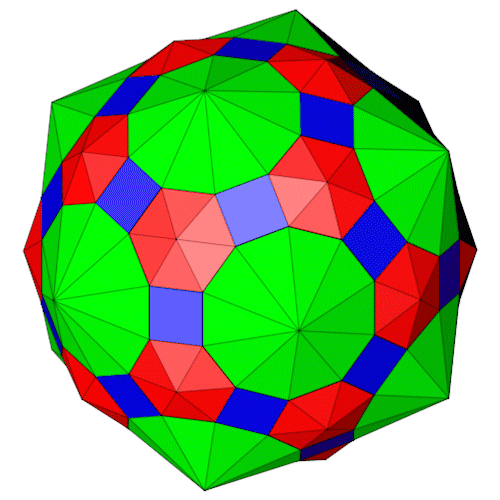
Das Große Rhombenikosidodekaeder leitet sich vom Rhombentriakontaeder ab. Die 30 Quadrate des Großen Rhombenikosidodekaeders liegen auf den Rhomben des Rhombentriakontaeders. Durch passende Abstufung der Ecken des Rhombentriakontaeders wird dann das Große Rhombenikosidodekaeder gebildet. Dabei werden vom Rhombentriakontaeder 6-Eck- und 10-Eck Pyramiden abgezogen.
 |
 |
 |
 |
 |
 |
| Isometrie | Dimetrie |
Die drei Seitenansichten.
Das Große Rhombenikosidodekaeder mit seiner Umkugel.
Das Große Rhombenikosidodekaeder mit seiner Kantenkugel.
Das Große Rhombenikosidodekaeder (blau) mit seinem dualen Körper, dem Hexakisikosaeder (rot). Der duale Körper bildet auf den Flächen des Großen Rhombenikosidodekaeders gleichmäßige Pyramiden.
Die Koordinaten der Eckpunkte des Großen Rhombenikosidodekaeders lassen sich aus folgender Beziehung herleiten. Phi ist dabei der goldene Schnitt.
Daraus werden die 3 geraden Permutationen gebildet.
Durch Variation der Vorzeichen ergeben sich 120 Punkte, für die Kantenlänge a gilt.
Die gleiche Kantenlänge hat der Dodekaederstumpf.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |