3.13. Abgeschrägtes Dodekaeder
|
[zurück] | 3.13. Abgeschrägtes Dodekaeder |
[vor] | |
 |
 |
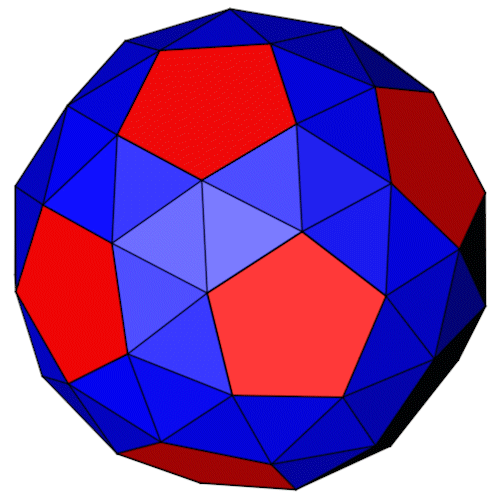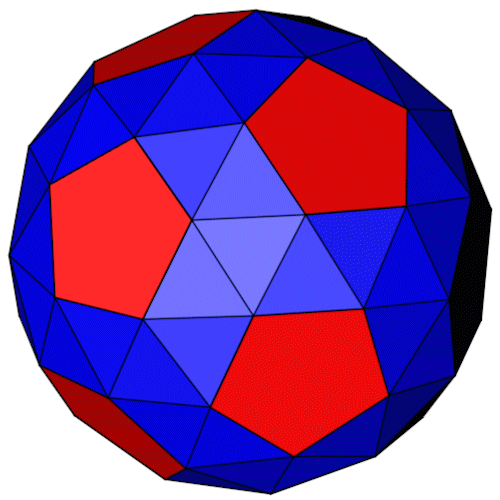
| Isometrie | Dimetrie |
| Name | Abgeschrägtes Dodekaeder Dodecaedron simum Snub dodecahedron |
| Anzahl Ecken | 60 |
| Anzahl Kanten | 150 |
| Anzahl Flächen | 80 Dreiecke 12 Fünfecke |
| Kantenlänge | 1 |
| Umkugelradius |  |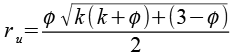
| Kantenkugelradius |  |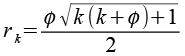
| Inkugelradius (Dreiecke) |  |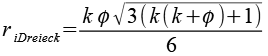
| Inkugelradius (Fünfecke) |  |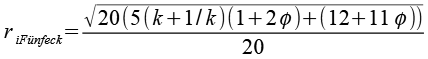
Mit
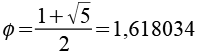und
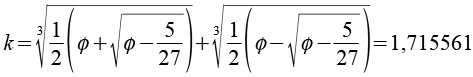
k ist eine Lösung der Gleichung
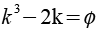
Der Umkugelradius ru ist eine Lösung der Gleichung
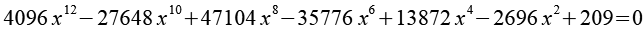
Die drei Seitenansichten.
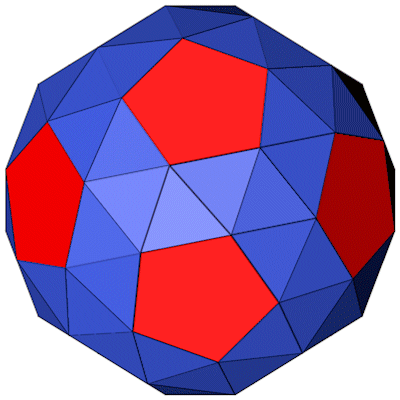
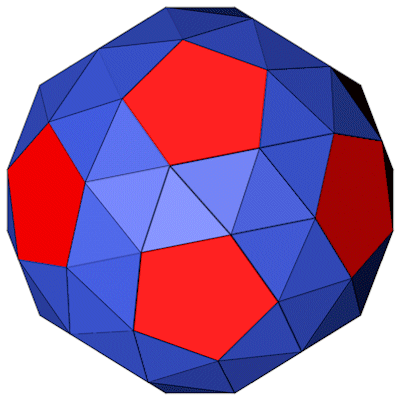
Das Abgeschrägte Dodekaeder mit seiner Umkugel.
Das Abgeschrägte Dodekaeder mit seiner Kantenkugel.
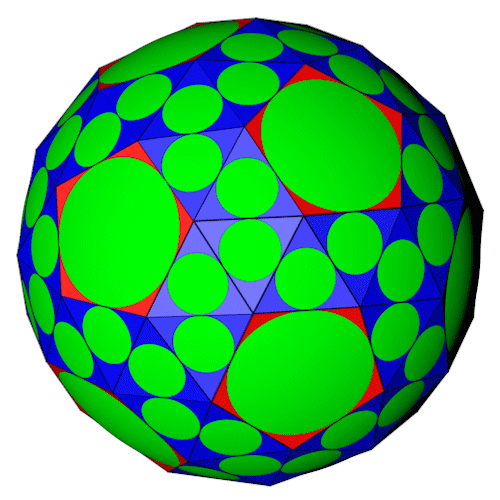
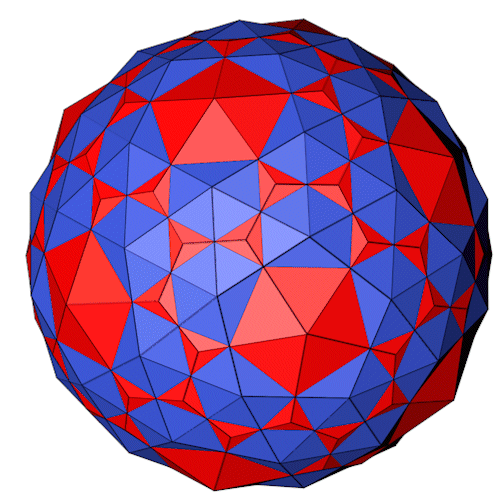
Das Abgeschrägte Dodekaeder (blau) mit seinem dualen Körper, dem Pentagonhexakontaeder (rot). Der duale Körper bildet auf den Flächen des Abgeschrägten Dodekaeders gleichmäßige Pyramiden.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |