| [zurück] | 2.1. Zylinder-Zylinder I |
[vor] |
Wir fangen erst einmal ganz einfach an indem wir zwei Zylinder betrachten die um 90 ° gegeneinander verdreht sind und deren Achsen in einer Ebene liegen. Für die Zylinder benutzen wir die parametrische Darstellung. Den Zylinder habe ich schon einmal in meinem Tutorial über Parametrische Flächen und Körper beschrieben.
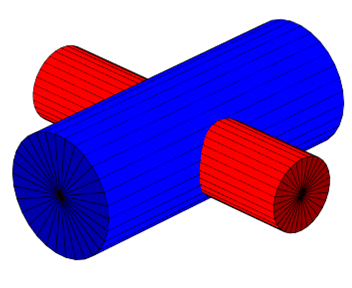
Abb. 3
Wir erzeugen einen Zylinder entlang der x-Achse (Radius R1) und einen entlang der z-Achse (Radius R2)
|
x = v1 |
9-1 |
|
|
y = R1 sin(u1) |
9-2 |
|
|
z = R1 cos(u1) |
9-3 |
|
|
x = R2 cos(u2) |
9-4 |
|
|
y = R2 sin(u2) |
9-5 |
|
|
z = v2 |
9-6 |
Wenn wir die Schnittlinien der beiden Zylinder berechnen wollen müssen wir die Gleichungen der Zylinder gleichsetzen.
|
v1 = R2 cos(u2) |
9-7 |
|
|
R1 sin(u1) = R2 sin(u2) |
9-8 |
|
|
R1 cos(u1) = v2 |
9-9 |
Jetzt haben wir 3 Gleichungen mit 4 Unbekannten (u1, v1, u2 und v2). Diese Anzahl müssen wir ein bischen reduzieren. Zuerst lösen wir Gl. 9-8 nach sin(u1) auf.
|
|
9-10 |
Die Sinusfunktion läßt sich auch durch die Cosinusfunktion ausdrücken. Für die Umwandlung benutzen wir Gl. 9-11 die wir in jeder Formelsammlung [1,2] finden können.
|
|
9-11 |
Wir setzen Gl. 9-10 in Gl. 9-11 ein und erhalten.
|
|
9-12 |
Jetzt setzen wir geschickt die gewonnenen Formeln in die Gleichung zur Erzeugung des ersten Zylinders ein. Zuerst setzten wir Gl. 9-7 in Gl. 9-1 ein.
|
x = R2 cos(u2) |
9-13 |
Jetzt setzen wir Gl. 9-10 in Gl. 9-2 ein.
|
y = R2 sin(u2) |
9-14 |
Zuletzt setzen wir Gl. 9-12 in Gl. 9-3 ein.
|
|
9-15 |
Gl. 9-15 können wir noch vereinfachen indem wir R1 mit in die Wurzel nehmen.
|
|
9-16 |
Jetzt haben wir für x, y und z Gleichungen die nur noch den Parameter u2 enthalten. Wir ersetzten u2 durch den Parameter t und erhalten die gewünschten Formeln für die Schnittlinie wie wir sie auch in der Literatur [5] finden können.
|
|
9-17 |

Abb. 4
In Abb. 4 sind die mit Gl. 9-17/18/19 berechneten Schnittlinien (t [0, 2 pi]) als Sweep-Nurbs (gelb) dargestellt. Da die Wurzel in Gl. 9-19 zwei Ergebnise liefert erhalten wir natürlich auch 2 Schnittlinien.
Auf der nächsten Seite wenden diese Formel einmal praktisch an.
| [zurück] | [Inhaltsverzeichnis] | [vor] |