| [zurück] | 3 Zylinder Sternmotor |
[vor] |
Sternmotoren wurden früher viel als Flugzeugmotoren verwendet da sie relativ leicht waren und ohne aufwändige Kühlung auskamen. Alle Zylinder wurde gleichmäßig vom Fahrtwind gekühlt. Heute finden sie fast nur noch im Modellbau Verwendung. Das ist eigentlich schade denn sie sehen faszinierend aus und es macht auch Spass die Cinema Animation zu verfolgen.

Ihr Funktionsprinzip unterscheidet sich von den anderen Kolbenmotoren. Alle Zylinder sind kreisförmig um die Kurbelwelle angeordnet. Obwohl es ein Mehrzylindermotor ist besitzt die Kurbelwelle nur einen Hubzapfen auf dem das sogenannte Mutterpleuel läuft. Alle anderen Kolben sind mit ihren Pleuelstangen am Mutterpleuel befestigt und nicht an der Kurbelwelle.
Die Animation des Mutterpleuels können wir einfach vom 1 Zylinder Motor stehend ableiten.

Bei den restlichen Pleuelstangen ist das nicht ganz so einfach. Die Berechnung ähnelt stark den V Motoren. Die Bewegung erfolgt aber relativ zum Mutterpleuel.
Da ich neben den 3 Zylinder Sternmotor auch einen 5 Zylinder und 7 Zylinder Sternmotor bauen möchte sollte die XPresso Berechnung so allgemein wie möglich sein um einfach weitere Zylinder anfügen zu können.
Wie beim V Motor benutzen wir den Sinussatz zur Berechnung der Winkel für die Tochterpleuel. Das Dreieck wird dabei aus dem beiden Lagerachsen des Tochterpleuels und dem Mittelpunkt der Kurbelwelle gebildet. Je nach Ausrichtung des Tochterpleuels müssen wir es in unterschiedliche Richtungen drehen. Die Bezugsachse für die Bewegung wird aus dem entsprechenden Kolben und dem Mittelpunkt der Kurbelwelle (Koordinatenursprung) gebildet. Zur Bildung dieser Achsen benutzen wir Kugeln als Dummyobjekte die wir in einigem Abstand um die Kurbelwelle gedreht haben (beim 3 Zylindermotor um 120°).
Wir kümmern uns erstmal nur um die Bewegung des Tochterpleuels. Zur Veranschaulichung eine kleine Skizze.
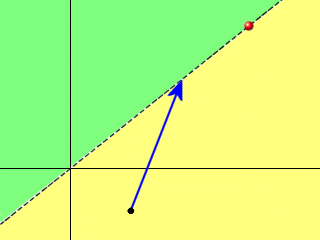
Die rote Kugel bestimmt die Richtung der Bewegung, der blaue Pfeil stellt das Tochterpleuel dar. Wenn wir das Tochterpleuel bewegen muss die Spitze immer auf der gestrichelten Linie bleiben. Für die Berechnung ist es wichtig zu wissen auf welcher Seite der Linie sich der Fußpunkt des Pleuels befindet, beide Seiten haben deshalb eine andere Farbe.
Wir fangen zuerst an für dieses logische Problem eine XGroup zu entwickeln. Zuerst wissen wir nur die Koordinaten der Kugel und die Koordinaten des Pleuels (Fußpunkt, schwarzer Punkt in der Skizze). Beide Koordinaten rechnen wir mit Hilfe der XGroup Polarkoordinaten in Polarkoordinaten um. So erhalten wir jeweils die Winkel und können sie vergleichen um die Lage des Pleuels zu bestimmen. Den Winkel zur Kugel bezeichnen wir mit Phi, den Winkel zum Pleuel mit Alpha. Dabei müssen wir zwischen positiven und negativen Werten für Phi unterscheiden. Für jeden Quadranten stellen wird einen Vergleich an.
Für negative Werte von Phi gilt
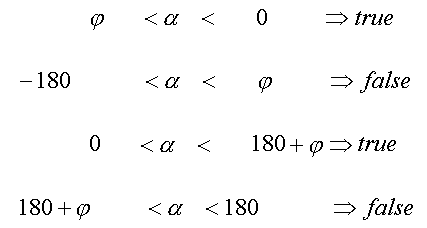
Die XGroup sieht dann so aus. Dabei benutzen wir auch die XGroup Bereich. Der obere Eingang ist für Alpha, der untere Eingang ist für Phi. Wir benutzen nur den ersten und den dritten Vergleich und die können wir noch zusammenfassen (Phi kleiner Alpha kleiner 180°+Phi).
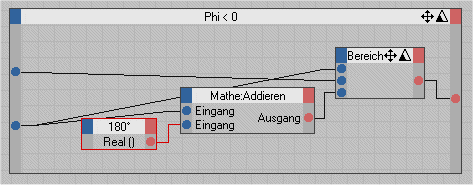
Für positive Werte von Phi gilt

Die XGroup sieht dann so aus.
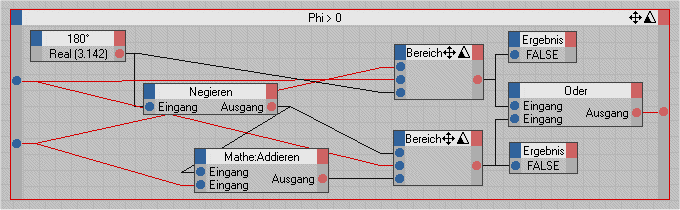
| [zurück] | [Inhaltsverzeichnis XPressostoffe] | [vor] |