| [zurück] | 3.83. Ei |
[vor] |
Als weiteres Beispiel für einen Rotationskörper erzeugen wir ein Ei. Die Funktion f(x) ist dann schon etwas komplizierter.
|
y = c sqrt(x (x - a) (x - b)) |
3-272 |
Mit den folgenden Gleichungen machen wir aus Gl. 3-272 einen Rotationskörper um die y-Achse.
|
x = c sqrt(u (u - a) (u - b)) sin(v) |
3-273 |
|
|
y = u |
3-274 |
|
|
z = c sqrt(u (u - a) (u - b)) cos(v) |
3-275 |
Zur besseren Übersicht die Gleichungen nochmal in normaler Schreibweise.
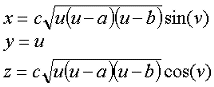
Die Konstanten a, b und c bestimmen das Aussehen der Figur. Dabei bestimmen a und b die Spitzheit des Eies, je geringer der Abstand zwischen a und b desto spitzer ist das Ei. Es muss aber die Bedingung a <= b eingehalten werden.
Zur Darstellung der Fläche können die beiden Parameter u und v zum Beispiel folgende Werte (Definitionsbereich) annehmen.
|
u ist Element aus der Zahlenmenge [0, a] |
||
|
v ist Element aus der Zahlenmenge [0, 2 pi] |
Beim Ei handelt es sich um eine geschlossene Figur, der Definitionsbereich kann daher beim Plugin nicht verändert werden.
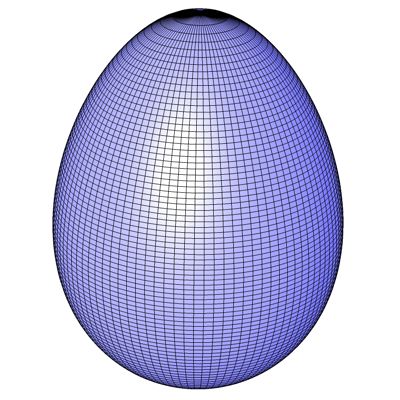
Abb. 88
Die Figur kann auf der nächsten Seite mit einem Java-Applet von allen Seiten betrachtet und gedreht werden.
| [zurück] | [Inhaltsverzeichnis] | [vor] |