| [zurück] | 3.80. Rotationskörper |
[vor] |
Aus einer Funktion y=f(x) in der x,y-Ebene läßt ich einfach ein Rotationskörper [33] erstellen.
|
y = f(x) |
3-260 |
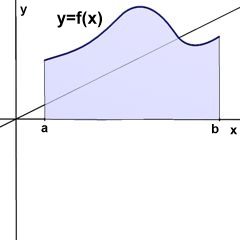
Abb. 84
Mit den folgenden Gleichungen machen wir aus Gl. 3-260 einen Rotationskörper um die x-Achse.
|
x = u |
3-261 |
|
|
y = f(u) sin(v) |
3-262 |
|
|
z = f(u) cos(v) |
3-263 |
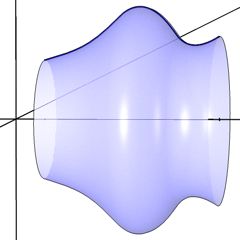
Abb. 85
Zur Darstellung der Fläche können die beiden Parameter u und v zum Beispiel folgende Werte (Definitionsbereich) annehmen.
|
u ist Element aus der Zahlenmenge [a, b] |
||
|
v ist Element aus der Zahlenmenge [0, 2 pi] |
| [zurück] | [Inhaltsverzeichnis] | [vor] |