| [zurück] | 7.1. Dodekaederstern |
[vor] |
Der Dodekaederstern leitet sich vom Dodekaeder ab, auf seine Fünfecke werden Fünfeckpyramiden gesetzt deren Kanten eine Verlängerung der Kanten der Fünfecke des Dodekaeders bilden. Die Spitzen der Pyramiden bilden einen Ikosaeder.
 |
 |
| Isometrie | Dimetrie |
| Name | Dodekaederstern Small stellated dodecahedron |
| Anzahl Ecken | 32 |
| Anzahl Flächen | 60 gleichschenklige Dreiecke |


Der Dodekaederstern mit dem Ikosaeder.

Der Dodekaederstern mit dem Dodekaeder.
Der Dodekaederstern mit der Umkugel des Dodekaeders.

Der Dodekaederstern mit seiner Umkugel.

Die 32 Punkte (Ecken) des Dodekaedersterns setzten sich aus den 20 Punkten des Dodekaeders und den 12 Punkten des Ikosaeders zusammen. Betrachten wir jeden Körper für sich.
Der Dodekaeders. Phi ist der goldene Schnitt.

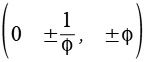
Für die Kantenlänge aD des Dodekaeders gilt.
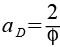
Der Ikosaeders.

Für die Kantenlänge aI des Ikosaeders gilt.
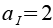
Für den Dodekaederstern muss der Ikosaeder natürlich größer sein, für die gesuchte Kantenlänge aIS gilt (Wikipedia)
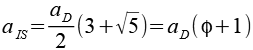
Setzen wir die Kantenlänge aD in die Formel ein.
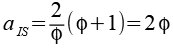
Unser "normale" Ikosaeder hat die Kantenlänge aI, der gesuchte Ikosaeder ist um den Faktor Phi größer. Wir müssen die Koordinaten des Ikosaeders daher mit Phi multiplizieren. Für den gesuchten Ikosaeder gilt dann.
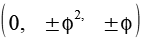
Für die Koordinaten des Dodekaederstern gilt dann.

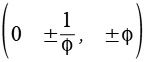
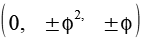
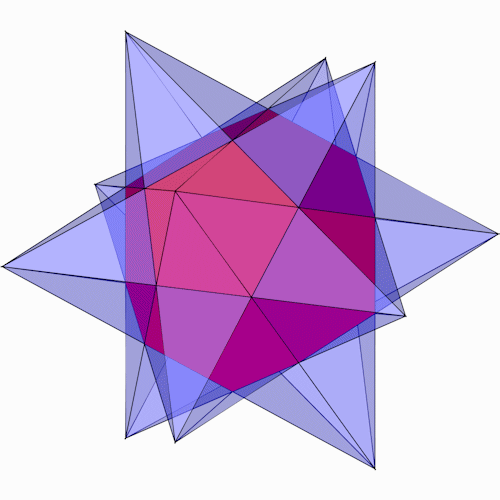
Der Dodekaederstern (blau) läßt sich mit dem Oktaeder (rot) kombinieren.


Der Dodekaederstern (blau) läßt sich mit dem Ikosaeder (rot) kombinieren.


| [zurück] | [Inhaltsverzeichnis] | [vor] |