Die Kanten eines Ikosaeders werden unterteilt und auf diese Punkte werden Kugeln gesetzt
(n Kugeln pro Kante), die Flächen (Dreiecke) werden entsprechend mit Kugeln ausgefüllt.
n = 2
12 Kugeln auf Kanten
 |
 |
| Isometrie |
Dimetrie |
n = 3
42 Kugeln auf Kanten
 |
 |
| Isometrie |
Dimetrie |
n = 4
72 Kugeln auf Kanten, 20 Kugeln auf Flächen
 |
 |
| Isometrie |
Dimetrie |
n = 5
102 Kugeln auf Kanten, 60 Kugeln auf Flächen
 |
 |
| Isometrie |
Dimetrie |
n = 6
132 Kugeln auf Kanten, 120 Kugeln auf Flächen
 |
 |
| Isometrie |
Dimetrie |
n = 7
162 Kugeln auf Kanten, 200 Kugeln auf Flächen
 |
 |
| Isometrie |
Dimetrie |
n = 8
192 Kugeln auf Kanten, 300 Kugeln auf Flächen
 |
 |
| Isometrie |
Dimetrie |
n = 9
222 Kugeln auf Kanten, 420 Kugeln auf Flächen
 |
 |
| Isometrie |
Dimetrie |
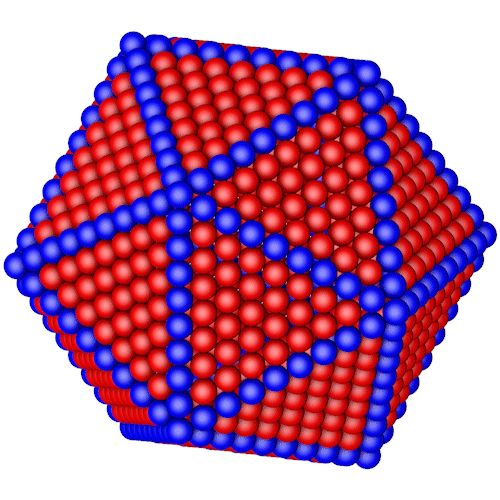
n = 10
252 Kugeln auf Kanten, 560 Kugeln auf Flächen
 |
 |
| Isometrie |
Dimetrie |
n = 11
282 Kugeln auf Kanten, 720 Kugeln auf Flächen
 |
 |
| Isometrie |
Dimetrie |
n = 12
312 Kugeln auf Kanten, 900 Kugeln auf Flächen
 |
 |
| Isometrie |
Dimetrie |





















