5.34. PCNH Methode
|
[zurück] | 5.34. PCNH Methode |
[vor] | |
Die PCNH Fraktale [2] werden nach folgender Formel berechnet. Zur Berechnung wird neben der Funktion f(zn) auch die erste Ableitung f '(zn) und die zweite Ableitung f ''(zn) benötigt, die Berechnung erfolgt in drei Stufen. Die erste Stufe yn entspricht der Newton Methode, die zweite Stufe n entspricht der Halley Methode und die dritte Stufe zn+1 entspricht der Householder Methode.
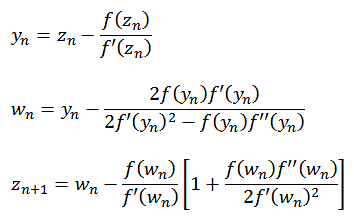
f(z) = z2 - 1
Nullstellen:
z1 = -1,0
z2 = 1,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Auch bei einem Polynom mit nur zwei Nullstellen gibt es eine Feinstruktur.
Die folgende Abbildung zeigt einen Bereich real [-0,65 bis 0,65] und imaginär [-0,65 bis 0,65].
f(z) = z3 - 1
Nullstellen:
z1 = -0,5 + 0,866025403784i
z2 = -0,5 - 0,866025403784i
z3 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = z4 - 5 z2 + 4
Nullstellen:
z1 = 1
z2 = -1
z3 = 2
z4 = -2
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [1,27 bis 1,65] und imaginär [-0,19 bis 0,19].
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |