5.1. Newton Methode
|
[zurück] | 5.1. Newton Methode |
[vor] | |
Die Newton Fraktale werden nach folgender Formel berechnet. Zur Berechnung wird neben der Funktion f(zn) auch die erste Ableitung f '(zn) benötigt.
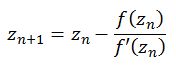
f(z) = z2 - 1
Nullstellen:
z1 = -1,0
z2 = 1,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Bei einem Polynom mit nur zwei Nullstellen ist das Bild trivial.
f(z) = z2 - z - 2
Nullstellen:
z1 = -1,0
z2 = 2,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Bei einem Polynom mit nur zwei Nullstellen ist das Bild trivial.
f(z) = z4 - 2 z3 - 3 z2 + 4 z + 4
Nullstellen:
z1,2 = -1,0
z3,4 = 2,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Die doppelten Nullstellen führen zu keinen Veränderungen, das Bild bleibt trivial.
f(z) = z3 - 1
Nullstellen:
z1 = -0,5 + 0,866025403784i
z2 = -0,5 - 0,866025403784i
z3 = 1,0 + 0,0i
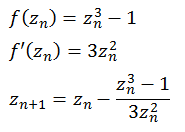
Die folgende Abbildung zeigt einen Bereich real [-1,8 bis 1,8] und imaginär [-1,8 bis 1,8].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [-0,8 bis 0,0] und imaginär [-0,3 bis 0,3].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [ bis ] und imaginär [ bis ].
Die folgenden beiden Abbildungen zeigen einen etwas anderen Algorithmus, die Nullstellen müssen dazu nicht bekannt sein. Die Iteration erfolgt so lange bis die Differenz zweier aufeinanderfolgender Werte kleiner einer Grenze ist. Die Farbe wird nach der Iterationstiefe ausgewählt. Berechnet wurde 2 bis 20 Iterationen.
Hier erfolgte die Farbgebung alternierend blau und weiß.
Die folgende Abbildung zeigt zusätzlich eine "Binary decomposition". Die Iterationstiefe beträgt 14 und bei der "Binary decomposition" 10. Die "Binary decomposition" erfolgt interessanterweise nur bei der realen Nullstelle.
Diese Berechnung läßt sich auch mit der "Distance estimation" Methode durchführen. Dazu wandeln wir die Formel für die Newton Methode
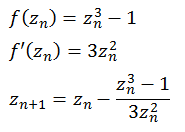
so um das wir nur einen Bruch haben. Diesem Bruch differenzieren wir um die erste Ableitung zu bekommen.
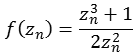
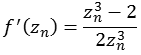
Die folgende Abbildung zeigt einen Bereich real [-1,0 bis 1,0] und imaginär [-1,0 bis 1,0].
f(z) = z4 - 1
Nullstellen:
z1 = 1.0 + 0.0i
z2 = -1.0 + 0.0i
z3 = 0.0 + 1.0i
z4 = 0.0 - 1.0i
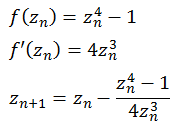
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
f(z) = z5 - 1
Nullstellen:
z1 = -0,809016994375 + 0,587785252292i
z2 = -0,809016994375 - 0,587785252292i
z3 = 0,309016994375 + 0,951056516295i
z4 = 0,309016994375 - 0,951056516295i
z5 = 1,0
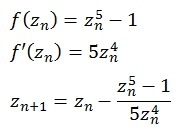
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [-0,86 bis 0,0] und imaginär [-0,3 bis 0,3].
Die folgende Abbildung zeigt zusätzlich eine "Binary decomposition". Die Iterationstiefe beträgt 30 (rot), 15 (blau) und bei der "Binary decomposition" 8. Die "Binary decomposition" erfolgt interessanterweise nur bei der realen Nullstelle.
f(z) = z3 - z
Nullstellen:
z1 = 1
z2 = 0
z3 = -1
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt zusätzlich eine "Binary decomposition". Die Iterationstiefe beträgt 13 (rot), 1 (blau) und bei der "Binary decomposition" 9. Die "Binary decomposition" erfolgt bei allen Nullstellen.
Die folgende drei Abbildungen zeigt einen Ausschnitt des letzten Bildes.
f(z) = z4 - 5 z2 + 4
Nullstellen:
z1 = -2
z2 = -1
z3 = 1
z4 = 2
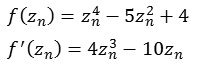
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [1,65 bis 1,45] und imaginär [-0,10 bis 0,10].
Die folgende Abbildung zeigt zusätzlich eine "Binary decomposition". Die Iterationstiefe beträgt 13 (rot), 9 (blau) und bei der "Binary decomposition" 8. Die "Binary decomposition" erfolgt bei allen Nullstellen.
f(z) = z7 - 14 z5 + 49 z3 - 36 z
Nullstellen:
z1 = -3
z2 = -2
z3 = -1
z4 = 0
z5 = 1
z6 = 2
z7 = 3
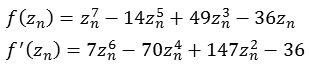
Die folgende Abbildung zeigt einen Bereich real [-3,5 bis 3,5] und imaginär [-3,5 bis 3,5].
Die folgende Abbildung zeigt einen Ausschnitt real [0,39 bis 0,66] und imaginär [-0,135 bis 0,135].
Die folgende Abbildung zeigt einen Ausschnitt real [1,45 bis 1,70] und imaginär [-0,125 bis 0,125].
Die folgende Abbildung zeigt einen Ausschnitt real [2,56 bis 2,71] und imaginär [-0,075 bis 0,075].
f(z) = 2 z3 - 2 z + 2
Nullstellen:
z1 = -1,32471795724 + 0,0i
z2 = 0,662358978622 + 0,562279512062i
z3 = 0,662358978622 - 0,562279512062i
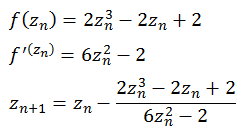
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [0,55 bis 0,90] und imaginär [-0,12 bis 0,12].
f(z) = z3 - 2 z + 2
Nullstellen:
z1 = -1,76929235424 + 0,0i
z2 = 0,884646177119 + 0,589742805022i
z3 = 0,884646177119 - 0,589742805022i
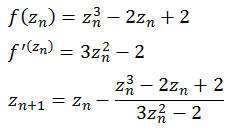
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5]. In dieser Abbildung gibt es Bereiche (weiße Flecken) in denen die Folge nicht zu einer der Nullstellen konvergiert, sie konvergiert dort gegen 0 oder 1.
Die folgende Abbildung zeigt zusätzlich eine "Binary decomposition". Die Iterationstiefe beträgt 15 (rot), 10 (blau) und bei der "Binary decomposition" 9. Die "Binary decomposition" erfolgt nur bei der realen Nullstelle.
Die folgende Abbildung zeigt einen Ausschnitt real [0,80 bis 1,05] und imaginär [-0,125 bis 0,125].
f(z) = z3 + c z - z - c
c = 0,30 + 1,64i
Nullstellen:
z1 = -1,39184135868 + 0,919446033786i
z2 = 0,391841358675 - 0,919446033786i
z3 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. In dieser Abbildung gibt es Bereiche (weiße Flecken) in denen die Folge nicht zu einer der Nullstellen konvergiert, sie konvergiert dort gegen zwei komplexe Zahlen.
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [-0,35 bis 0,35] und imaginär [-0,35 bis 0,35].
f(z) = z6 + z3 - 1
Nullstellen:
z1 = -0,42589982104 + 0,737680128975i
z2 = -0,42589982104 - 0,737680128975i
z3 = 0,586992498353 + 1,01670083081i
z4 = 0,586992498353 - 1,01670083081i
z5 = -1,17398499671
z6 = 0,851799642079
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
Die folgende Abbildung zeigt zusätzlich eine "Binary decomposition". Die Iterationstiefe beträgt 25 (rot), 15 (blau) und bei der "Binary decomposition" 10. Die "Binary decomposition" erfolgt nur bei den beiden realen Nullstellen.
f(z) = (z4 - 1)(z4 + 16) = z8 + 15 z4 - 16
Nullstellen:
z1 = 1
z2 = -1
z3 = i
z4 = -i
z5 = 1.41421356237 + 1.41421356237i
z6 = 1.41421356237 - 1.41421356237i
z7 = -1.41421356237 + 1.41421356237i
z8 = -1.41421356237 - 1.41421356237i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = (z4 - 1)(z4 + 4) = z8 + 3 z4 - 4
Nullstellen:
z1 = 1
z2 = -1
z3 = i
z4 = -i
z5 = 1 + i
z6 = 1 - i
z7 = -1 + i
z8 = -1 - i
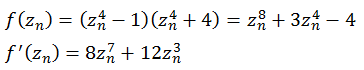
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-2,0 bis 2,0].
f(z) = z4 - 4,29 z2 - 5,29
Nullstellen:
z1 = 2,3
z2 = -2,3
z3 = i
z4 = -i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. In dieser Abbildung gibt es Bereiche (weiße Flecken) in denen die Folge nicht zu einer der Nullstellen konvergiert, sie konvergiert dort gegen -0,7876 oder 0,7876.
f(z) = (z4 - 1)(z4 - 16) = z8 - 17 z4 + 16
Nullstellen:
z1 = 1
z2 = -1
z3 = i
z4 = -i
z5 = 2
z6 = -2
z7 = 2i
z8 = -2i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
a = -0,00508 + 0,33136i
Nullstellen:
z1 = -0,5 - Re(a) + Im(a)i
z2 = -0,5 + Re(a) - Im(a)i
z3 = 1
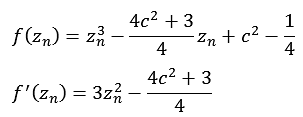
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-2,0 bis 2,0].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [-0,25 bis 0,25] und imaginär [-0,25 bis 0,25].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [-0,11 bis 0,11] und imaginär [-0,0825 bis 0,0825].
f(z) = cos(z)
Die folgende Abbildung zeigt einen etwas anderen Algorithmus, die Nullstellen müssen dazu nicht bekannt sein. Die Iteration erfolgt so lange bis die Differenz zweier aufeinanderfolgender Werte kleiner einer Grenze ist. Die Farbe wird nach der Iterationstiefe ausgewählt. Dargestellt wird ein Bereich real [-0,50 bis 0,50] und imaginär [-0,50 bis 0,50].
f(z) = z3 + c*z - z - c
Bei diesem Beispiel wird nicht die Varianle z sondern die Konstante c bei der Berechnung verändert. Dabei entstehen Zonen in Form eines Apfelmännchens in denen die Berechnung nicht konvergiert.
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 1,5] und imaginär [-2,0 bis 2,0]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (50, 13, 16 und 10).
Die folgende Abbildung zeigt einen Ausschnitt des ersten Bildes im Bereich real [-0,3 bis 0,5] und imaginär [1,4 bis 2,0]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (50, 15, 20 und 12).
Die folgende Abbildung zeigt einen Ausschnitt des ersten Bildes im Bereich real [0,08 bis 0,12] und imaginär [1,85 bis 1,89].
Die Berechnung habe ich mit einem etwas anderen Algorithmus wiederholt, die folgende Abbildung zeigt einen Ausschnitt im Bereich real [-2,35 bis 1,65] und imaginär [-2,00 bis 2,00].
Die folgende Abbildung zeigt einen Bereich real [-0,20 bis 0,40] und imaginär [1,40 bis 2,00].
Die folgende Abbildung zeigt einen Bereich real [0,092 bis 0,112] und imaginär [1,859 bis 1,879].
Das "Apfelmänmnchen" in der Mitte habe ich separat rot gefärbt.
In den blauen Zonen konvergiert die Berechnung gegen 1, in den weißen konvergiert er gegen eine Zahl ungleich 1. In der Zone des "Apfelmänmnchen" konvergiert die Berechnung nicht gegen eine Konstante, sondern pendelt zwischen zwei Werten. Um das zu verdeutlichen habe ich in der folgenden Abbildung 6 Punkte eingezeichnet, je zwei in einer der drei Zonen.
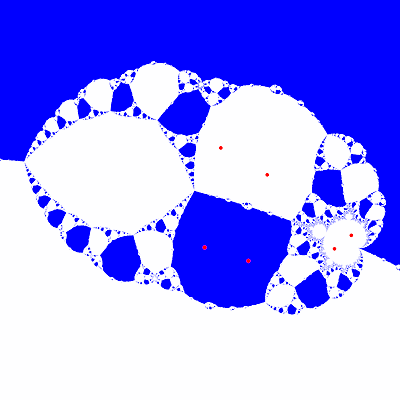
Für jeden dieser 6 Punkte habe ich die Berechnung der ersten Zyklen in einem Diagramm dargestellt.
Beide Werte konvergieren gegen 1.
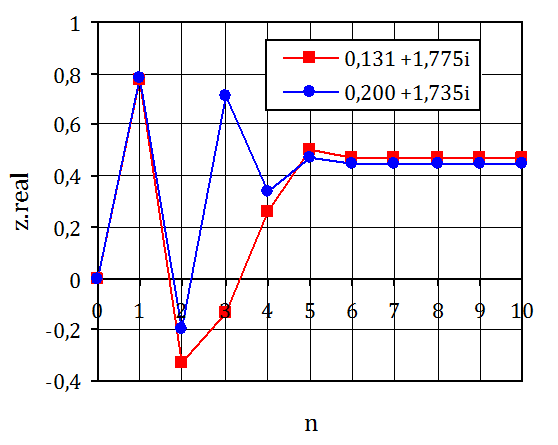
Beide Werte konvergieren gegen verschiedene Zahlen.
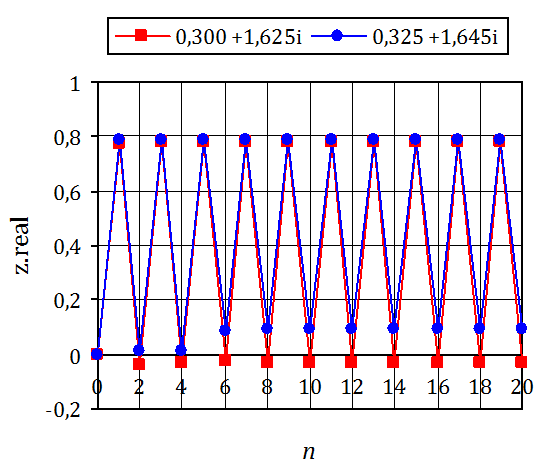
Beide Werte konvergieren nicht gegen eine Zahl sondern pendeln zwischen zwei Werten.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |