5.1. Newton Methode
|
[zurück] | 5.1. Newton Methode |
[vor] | |
f(z) = za - 1
Auch bei gebrochenen Exponenten [8] läßt sich das Newton Verfahren anwenden und man erhält interessante Ergebnisse. Die Berechnung erfolgt nach folgender Formel. Um eine hohe Auflösung zu gewährleisten wurde die Iterationstiefe von sonst 100 auf 5000 heraufgesetzt, das führte zu extrem langen Rechenzeiten von ca. 24 Stunden pro Bild. Da kommt ein Python Interpreter an seine Grenzen, trotz i7 4770 mit 3,4 GHz.
Nullstellen für a = 3,3:
z1 = -0,327067963317 + 0,945000818715i
z2 = -0,327067963317 - 0,945000818715i
z3 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Nullstellen für a = 3,88221:
z1 = -0,0476414368456 + 0,99886450207i
z2 = -0,0476414368456 - 0,99886450207i
z3 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Nullstellen für a = 3,88222:
z1 = -0,0476372726864 + 0,998864700673i
z2 = -0,0476372726864 - 0,998864700673i
z3 = 1,0 + 0,0i
Schon kleine Änderungen des Exponenten haben eine große Wirkung. Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. In den weissen Bereichen konvergiert die Berechnung zu keiner Nullstelle.
Die folgende Formel habe ich hier [4] gefunden.
f(z) = arcsin(z)2 - c
Komplexe trigonometrische Funktionen ergeben schöne Muster.
Betrachten wir zuerst die Ableitung von arcsin(z).
Zur Berechnung der Ableitung von f(z) = arcsin(z)2 - c müssen wir die Kettenregel bemühen.
Zur Kontrolle habe ich die Ableitung auch über die Produktregel berechnet. Auf die Konstante c kann verzichtet werden.
c = 0,5
Die folgende Abbildung zeigt einen Bereich real [-7,0 bis 7,0] und imaginär [-7,0 bis 7,0]. Dargestellt werden 4 verschiedene Iterationstiefen.
Die folgende Abbildung zeigt einen Bereich real [-7,0 bis 7,0] und imaginär [-7,0 bis 7,0]. Dargestellt werden 4 verschiedene Iterationstiefen, zusätzlich erfolgte eine "Binary decomposition" in den weißen Bereichen.
c = 1,0
Die folgende Abbildung zeigt einen Bereich real [-7,0 bis 7,0] und imaginär [-7,0 bis 7,0]. Die Iterationstiefe betrug 40.
Die folgende Abbildung zeigt einen Bereich real [-7,0 bis 7,0] und imaginär [-7,0 bis 7,0]. Die Iterationstiefe betrug 40, zusätzlich erfolgte eine "Binary decomposition" in den weißen Bereichen.
f(z) = z6 - z3 - 2
Nullstellen:
z1 = -0.134880231841 +1.11432866469i
z2 = -0.134880231841 -1.11432866469i
z3 = -0.897596815867 +0.673974039589i
z4 = -0.897596815867 -0.673974039589i
z5 = 1.03247704771 +0.440354625103i
z6 = 1.03247704771 -0.440354625103i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [0,76 bis 1,12] und imaginär [-0,18 bis 0,18].
f(z) = z3 - z - 1
Nullstellen:
z1 = -0,66235897862 +0,56227951206i
z2 = -0,66235897862 -0,56227951206i
z3 = 1,32471795724
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = 600 z4 - 550 z3 + 200 z2 - 20 z - 1
Nullstellen:
z1 = 0,23235296475
z2 = -0,0358396918663
z3 = 0,360076696892 +0,265491739908i
z4 = 0,360076696892 -0,265491739908i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = z6 - a z4 - z2 + a
Nullstellen:
z1 = 1,0 +1,0i
z2 = -1,0 -1,0i
z3 = 1,0
z4 = -1,0
z5 = 1,0i
z6 = -1,0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = za - az
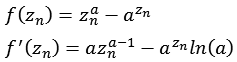
a = 3
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [-0,75 bis -0,40] und imaginär [-0,175 bis 0,175].
a = 4
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Dargestellt sind Iterationgrade von 2 bis 12.
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Dargestellt sind Iterationgrade von 2 bis 10.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |