5.3. Halley Methode
|
[zurück] | 5.3. Halley Methode |
[vor] | |
Die Halley Fraktale [41, 59] werden nach folgender Formel berechnet. Zur Berechnung wird neben der Funktion f(zn) auch die erste Ableitung f '(zn) und die zweite Ableitung f ''(zn) benötigt.
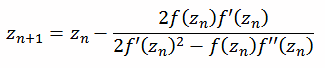
Die Halley Formel kann man auch anders darstellen.
mit (siehe Whittaker Methode)
Durch Einsetzen erhält man wieder die ursprüngliche Formel.
f(z) = z2 - 1
Nullstellen:
z1 = -1,0
z2 = 1,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Bei einem Polynom mit nur zwei Nullstellen ist das Bild trivial.
f(z) = z2 - z - 2
Nullstellen:
z1 = -1,0
z2 = 2,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Bei einem Polynom mit nur zwei Nullstellen ist das Bild trivial.
f(z) = z4 - 2 z3 - 3 z2 + 4 z + 4
Nullstellen:
z1,2 = -1,0
z3,4 = 2,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Die doppelten Nullstellen führen zu keinen Veränderungen, das Bild bleibt trivial.
f(z) = z3 - 1
Nullstellen:
z1 = -0,5 + 0,866025403784i
z2 = -0,5 - 0,866025403784i
z3 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [-1,3 bis -0,7] und imaginär [-0,3 bis 0,3].
f(z) = z4 - 1
Nullstellen:
z1 = 1.0 + 0.0i
z2 = -1.0 + 0.0i
z3 = 0.0 + 1.0i
z4 = 0.0 - 1.0i
Die folgende Abbildung zeigt einen Bereich real [-1,0 bis 1,0] und imaginär [-1,0 bis 1,0].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [0,5 bis 0,9] und imaginär [0,5 bis 0,9].
f(z) = z5 - 1
Nullstellen:
z1 = -0,809016994375 + 0,587785252292i
z2 = -0,809016994375 - 0,587785252292i
z3 = 0,309016994375 + 0,951056516295i
z4 = 0,309016994375 - 0,951056516295i
z5 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-1,3 bis 1,3] und imaginär [-1,3 bis 1,3].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [-1.1450 bis -0.8450] und imaginär [-0.15 bis 0.15].
f(z) = 2 z3 - 2 z + 2
Nullstellen:
z1 = -1,32471795724 + 0,0i
z2 = 0,662358978622 + 0,562279512062i
z3 = 0,662358978622 - 0,562279512062i
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [0.875 bis 1.075] und imaginär [-0.1 bis 0.1].
f(z) = z3 - 2 z + 2
Nullstellen:
z1 = -1,76929235424 + 0,0i
z2 = 0,884646177119 + 0,589742805022i
z3 = 0,884646177119 - 0,589742805022i
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
f(z) = z4 - 5 z2 + 4
Nullstellen:
z1 = 1
z2 = -1
z3 = 2
z4 = -2
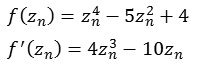
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = z6 - z3 - 2
Nullstellen:
z1 = -0.134880231841 +1.11432866469i
z2 = -0.134880231841 -1.11432866469i
z3 = -0.897596815867 +0.673974039589i
z4 = -0.897596815867 -0.673974039589i
z5 = 1.03247704771 +0.440354625103i
z6 = 1.03247704771 -0.440354625103i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = (z4 - 1)(z4 + 16) = z8 + 15 z4 - 16
Nullstellen:
z1 = 1
z2 = -1
z3 = i
z4 = -i
z5 = 1.41421356237 + 1.41421356237i
z6 = 1.41421356237 - 1.41421356237i
z7 = -1.41421356237 + 1.41421356237i
z8 = -1.41421356237 - 1.41421356237i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = (z4 - 1)(z4 - 16) = z8 - 17 z4 + 16
Nullstellen:
z1 = 1
z2 = -1
z3 = i
z4 = -i
z5 = 2
z6 = -2
z7 = 2i
z8 = -2i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = z3 - z
Nullstellen:
z1 = 1
z2 = 0
z3 = -1
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = cos(z)
Die folgende Abbildung zeigt einen etwas anderen Algorithmus, die Nullstellen müssen dazu nicht bekannt sein. Die Iteration erfolgt so lange bis die Differenz zweier aufeinanderfolgender Werte kleiner einer Grenze ist. Die Farbe wird nach der Iterationstiefe alternierend ausgewählt. Dargestellt wird ein Bereich real [-2,50 bis 2,50] und imaginär [-2,50 bis 2,50].
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [-0,5 bis 0,5] und imaginär [0,4 bis 1,4].
f(z) = 600 z4 - 550 z3 + 200 z2 - 20 z - 1
Nullstellen:
z1 = 0,23235296475
z2 = -0,0358396918663
z3 = 0,360076696892 +0,265491739908i
z4 = 0,360076696892 -0,265491739908i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = z6 - a z4 - z2 + a
Nullstellen:
z1 = 1,0 +1,0i
z2 = -1,0 -1,0i
z3 = 1,0
z4 = -1,0
z5 = 1,0i
z6 = -1,0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [-0,4 bis -0,1] und imaginär [-0,4 bis -0,1].
Die folgende Abbildung zeigt einen Bereich real [0,42 bis 0,57] und imaginär [1,05 bis 1,20].
Um zu anderen interessanten Bildern zu kommen habe ich die Formel ein bischen modifiziert. Dabei hatte ich folgender Formel verwendet.
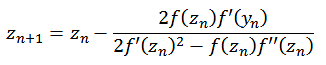
mit
f(z) = z2 - 1
Nullstellen:
z1 = -1,0
z2 = 1,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = z3 - 1
Nullstellen:
z1 = -0,5 + 0,866025403784i
z2 = -0,5 - 0,866025403784i
z3 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = z4 - 5 z2 + 4
Nullstellen:
z1 = 1
z2 = -1
z3 = 2
z4 = -2
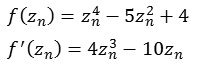
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |