5.69. Matinfar-Aminzadeh Methode
|
[zurück] | 5.69. Matinfar-Aminzadeh Methode |
[vor] | |
Die Matinfar-Aminzadeh Fraktale [58] werden nach folgender Formel berechnet. Zur Berechnung wird neben der Funktion f(zn) auch die erste Ableitung f '(zn) benötigt.
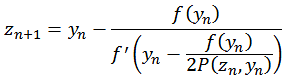
mit
und
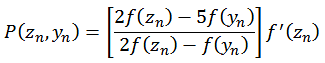
f(z) = z2 - 1
Nullstellen:
z1 = -1,0
z2 = 1,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Auch bei einem Polynom mit nur
zwei Nullstellen gibt es eine Feinstruktur.
Diese kleinen kreisrunden Strukturen habe ich sonst nur bei der Feng Methode und der
Changbum-Chun II Methode gefunden.
f(z) = z3 - 1
Nullstellen:
z1 = -0,5 + 0,866025403784i
z2 = -0,5 - 0,866025403784i
z3 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [0,375 bis 0,505] und imaginär [-0,065 bis 0,065].
Die folgende Abbildung zeigt einen Bereich real [-0,527 bis -0,573] und imaginär [-0,023 bis 0,023].
f(z) = z4 - 1
Nullstellen:
z1 = 1.0 + 0.0i
z2 = -1.0 + 0.0i
z3 = 0.0 + 1.0i
z4 = 0.0 - 1.0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [0,52 bis 0,64] und imaginär [-0,06 bis 0,06].
f(z) = z3 - z
Nullstellen:
z1 = 1
z2 = 0
z3 = -1
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [0,47 bis 0,72] und imaginär [-0,125 bis 0,125].
Die folgende Abbildung zeigt einen Bereich real [0,533 bis 0,583] und imaginär [0,596 bis 0,646].
f(z) = z4 - 5 z2 + 4
Nullstellen:
z1 = 1
z2 = -1
z3 = 2
z4 = -2
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [-0,27 bis 0,27] und imaginär [-0,27 bis 0,27].
Die folgende Abbildung zeigt einen Bereich real [0,1907 bis 0,1963] und imaginär [-0,0028 bis 0,0028].
Die folgende Abbildung zeigt einen Bereich real [1,50 bis 1,72] und imaginär [-0,11 bis 0,11].
Die folgende Abbildung zeigt einen Bereich real [1,5521 bis 1,5541] und imaginär [-0,001 bis 0,001].
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |