5.61. Feng Methode
|
[zurück] | 5.61. Feng Methode |
[vor] | |
Die Feng Fraktale [49] werden nach folgender Formel berechnet. Zur Berechnung wird neben der Funktion f(zn) auch die erste Ableitung f '(zn) benötigt.
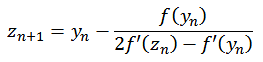
mit
f(z) = z2 - 1
Nullstellen:
z1 = -1,0
z2 = 1,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Auch bei einem Polynom mit nur
zwei Nullstellen gibt es eine Feinstruktur.
Diese kleinen kreisrunden Strukturen habe ich sonst nur bei der
Matinfar-Aminzadeh Methode und der
Changbum-Chun II Methode gefunden.
Die folgende Abbildung zeigt einen Bereich real [0,565 bis 0,655] und imaginär [-0,045 bis 0,045].
f(z) = z3 - 1
Nullstellen:
z1 = -0,5 + 0,866025403784i
z2 = -0,5 - 0,866025403784i
z3 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
Die folgende Abbildung zeigt einen Bereich real [0,755 bis 0,791] und imaginär [-0,018 bis 0,018].
f(z) = z4 - 1
Nullstellen:
z1 = 1.0 + 0.0i
z2 = -1.0 + 0.0i
z3 = 0.0 + 1.0i
z4 = 0.0 - 1.0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [-0,87 bis -0,83] und imaginär [-0,02 bis 0,02].
Die folgende Abbildung zeigt einen Bereich real [0,45 bis 0,53] und imaginär [0,315 bis 0,395].
f(z) = z4 - 5 z2 + 4
Nullstellen:
z1 = 1
z2 = -1
z3 = 2
z4 = -2
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [-0,45 bis 0,45] und imaginär [-0,45 bis 0,45].
Die folgende Abbildung zeigt einen Bereich real [1,33 bis 1,60] und imaginär [-0,135 bis 0,135].
Die folgende Abbildung zeigt einen Bereich real [1,851 bis 1,871] und imaginär [-0,01 bis 0,01].
f(z) = (z4 - 1)(z4 + 16) = z8 + 15 z4 - 16
Nullstellen:
z1 = 1
z2 = -1
z3 = i
z4 = -i
z5 = 1.41421356237 + 1.41421356237i
z6 = 1.41421356237 - 1.41421356237i
z7 = -1.41421356237 + 1.41421356237i
z8 = -1.41421356237 - 1.41421356237i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [0,845 bis 0,883] und imaginär [-0,019 bis 0,019].
f(z) = z3 - z
Nullstellen:
z1 = 1
z2 = 0
z3 = -1
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [0,30 bis 0,60] und imaginär [-0,15 bis 0,15].
Die folgende Abbildung zeigt einen Bereich real [0,4190 bis 0,4245] und imaginär [-0,00275 bis 0,00275].
Die folgende Abbildung zeigt einen Bereich real [0,49505 bis 0,49575] und imaginär [-0,00035 bis 0,00035].
f(z) = z5 - 5 z3 + 4 z
Nullstellen:
z1 = -2
z2 = -1
z3 = 0
z4 = 1
z5 = 2
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [0,30 bis 0,90] und imaginär [-0,30 bis 0,30].
Die folgende Abbildung zeigt einen Bereich real [0,480 bis 0,496] und imaginär [-0,008 bis 0,008].
Die folgende Abbildung zeigt einen Bereich real [-1,77 bis -1,43] und imaginär [-0,17 bis 0,17].
Die folgende Abbildung zeigt einen Bereich real [1,883 bis 1,901] und imaginär [-0,009 bis 0,009].
Die folgende Abbildung zeigt einen Bereich real [0,7080 bis 0,7105] und imaginär [-0,00125 bis 0,00125].
Die folgende Abbildung zeigt einen Bereich real [1,89521 bis 1,89530] und imaginär [-0,000045 bis 0,000045].
f(z) = 600 z4 - 550 z3 + 200 z2 - 20 z - 1
Nullstellen:
z1 = 0,23235296475
z2 = -0,0358396918663
z3 = 0,360076696892 +0,265491739908i
z4 = 0,360076696892 -0,265491739908i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |