| [zurück] | 3.1. zn+1 = zn2 + c (Apfelmännchen) |
[vor] |
Das "Apfelmännchen" wird nach folgender Formel berechnet.
![]()
![]()
Mit Hilfe der Kardioide lassen sich die Positionen der "Knospen" auf der Oberflächen des Apfelmännchens berechnen. Den dabei
verwendeten Brüchen entsprichen den periodischen Zyklen der "Knospen".
Die folgenden Abbildungen wurden entsprechend der Brüche berechnet. Für den Parameter t = 1/3 der Kardioide erhält man eine Knospe
mit der Periodizität 3. Der Körper der Knospe wurde mit der "Escape Time" Methode berechnet (blau), die feinen Strukturen mit
der "Distance estimation" Methode (rot). So lassen sich die Anzahl der Perioden gut darstellen. Bei 1/3 sind es drei Strahlen,
bei 1/7 sind es 7 Strahlen. Mit einem Zahlenwert aus der Mitte der "Knospe" wure auch die entsprechende Julia Menge berechnet,
hier findet man die gleiche Periode.
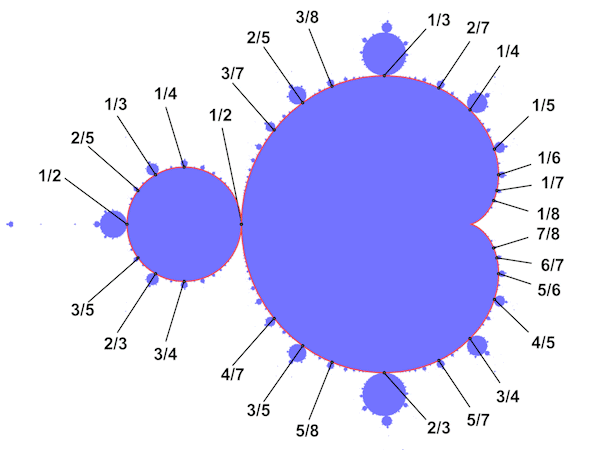
Die Ordnung der Knospen ergibt sich aus der "Summe" der beiden benachbarten größeren Knospen.
 |
 |
|
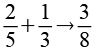 |
 |
Parametrische Darstellung der Kardioide.
![]()

Parametrische Darsttellung des Kreises.
![]()
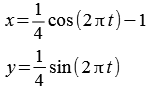
1/3
Die folgende Abbildung zeigt einen Bereich real [-0,35 bis 0,10] und imaginär [0,65 bis 1,10].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = -0,125 + 0,750i.
1/4
Die folgende Abbildung zeigt einen Bereich real [0,20 bis 0,45] und imaginär [0,45 bis 0,70].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = 0,282 + 0,532i.
1/5
Die folgende Abbildung zeigt einen Bereich real [0,350 bis 0,500] und imaginär [0,275 bis 0,425].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = 0,378 + 0,336i.
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = 0,408 + 0,340i, einem Punkt aus dem Kopf der "Knospe". Die Julia Menge wird filigraner aber zeigt die gleiche Periode.
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = 0,4158 + 0,3407i, einem Punkt aus dem Kopf des Kopfes. Die Julia Menge wird noch filigraner aber zeigt die gleiche Periode.
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = 0,4260 + 0,3413i, einem Punkt aus dem separaten kleinen Apfelmännchen rechts neben der Knospe. Die Julia Menge wird noch filigraner aber zeigt die gleiche Periode, die Struktur ist aber kaum noch zu sehen.
Die folgende Abbildung zeigt eine Vergrößerung des letzten Bildes, einen Bereich real [-0,40 bis 0,40] und imaginär [-0,40 bis 0,40] für c = 0,4260 + 0,3413i. Um die feine Struktur besser darstellen zu können wurde zusätzlich die "Distance estimation" Methode (rot) verwendet.
2/5
Die folgende Abbildung zeigt einen Bereich real [-0,65 bis -0,40] und imaginär [0,50 bis 0,75].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = -0,505 + 0,565i.
1/6
Die folgende Abbildung zeigt einen Bereich real [0,36 bis 0,46] und imaginär [0,27 bis 0,17].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = 0,389 + 0,217i.
1/7
Die folgende Abbildung zeigt einen Bereich real [0,36 bis 0,42] und imaginär [0,11 bis 0,17].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = 0,375 + 0,145i.
3/7
Die folgende Abbildung zeigt einen Bereich real [-0,7 bis -0,6] und imaginär [0,4 bis 0,5].
Die folgende Abbildung zeigt einen Bereich real [-0,667 bis -0,651] und imaginär [0,442 bis 0,458].
Die folgende Abbildung zeigt einen Bereich real [-0,66178 bis -0,65613] und imaginär [0,44722 bis 0,45287].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = -0,622 + 0,425i.
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = -0,65857 + 0,44988i, einem Punkt aus dem separaten Apfelmännchen.
Die folgende Abbildung zeigt einen Bereich real [-0,40 bis 0,40] und imaginär [-0,30 bis 0,30] für c = -0,65857 + 0,44988i.
Die folgende Abbildung zeigt einen Bereich real [-0,10 bis 0,10] und imaginär [-0,10 bis 0,10] für c = -0,65857 + 0,44988i. Es ist schon verblüffend wie sich die Bilder der Mandelbrot- und Juliamenge in der Vergrößerung gleichen.
4/9
Die folgende Abbildung zeigt einen Bereich real [-0,75 bis -0,65] und imaginär [0,30 bis 0,40].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = -0,672 + 0,338i.
1/10
Die folgende Abbildung zeigt einen Bereich real [0,325 bis 0,345] und imaginär [0,040 bis 0,060].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = 0,3300 + 0,0543i.
5/11
Die folgende Abbildung zeigt einen Bereich real [-0,75 bis -0,68] und imaginär [0,25 bis 0,32].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = -0,698 + 0,280i.
1/12
Die folgende Abbildung zeigt einen Bereich real [0,305 bis 0,318] und imaginär [0,023 bis 0,036].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = 0,3090 + 0,0322i.
1/15
Die folgende Abbildung zeigt einen Bereich real [0,288 bis 0,294] und imaginär [0,012 bis 0,018].
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-1,5 bis 1,5] für c = 0,2900 + 0,0168i.
| [zurück] | [Inhaltsverzeichnis] | [vor] |