| [zurück] | 2.2. Zylinder-Zylinder II |
[vor] |
Jetzt erweitern wir unser mathematische Modell Zylinder-Zylinder I indem wir den 2. Zylinder entlang der y-Achse um den Offset a nach oben verschieben.
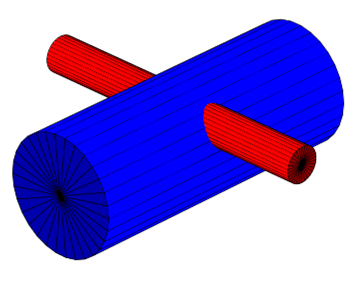
Abb. 12
An den Gleichungen des ersten Zylinders ändert sich nichts, beim zweiten Zylinder addieren wir den Offset a zu Gl. 9-5.
|
x = v1 |
9-1 |
|
|
y = R1 sin(u1) |
9-2 |
|
|
z = R1 cos(u1) |
9-3 |
|
|
x = R2 cos(u2) |
9-4 |
|
|
y = a + R2 sin(u2) |
9-20 |
|
|
z = v2 |
9-6 |
Wie beim ersten mal müssen wir die Gleichungen der Zylinder gleichsetzen.
|
v1 = R2 cos(u2) |
9-7 |
|
|
R1 sin(u1) = a + R2 sin(u2) |
9-21 |
|
|
R1 cos(u1) = v2 |
9-9 |
Jetzt lösen wir Gl. 9-21 nach sin(u1) auf.
|
|
9-22 |
Mit Hilfe von Gl. 9-11 drücken wir Gl. 9-22 als Cosinus aus.
|
|
9-23 |
Jetzt setzen wir geschickt die gewonnenen Formeln in die Gleichung zur Erzeugung des ersten Zylinders ein. Zuerst setzten wir Gl. 9-7 in Gl. 9-1 ein.
|
x = R2 cos(u2) |
9-13 |
Jetzt setzen wir Gl. 9-22 in Gl. 9-2 ein.
|
y = a + R2 sin(u2) |
9-24 |
Zuletzt setzen wir Gl. 9-23 in Gl. 9-3 ein.
|
|
9-25 |
Gl. 9-25 können wir noch vereinfachen indem wir R1 mit in die Wurzel nehmen.
|
|
9-26 |
Jetzt haben wir für x, y und z Gleichungen die nur noch den Parameter u2 enthalten. Wir ersetzten u2 durch den Parameter t und erhalten die gewünschten Formeln.
|
|
9-27 |
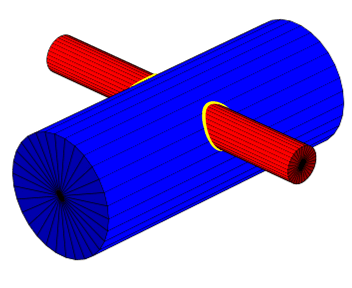
Abb. 13
In Abb. 13 sind die mit Gl. 9-27/28/29 berechneten Schnittlinien (t [0, 2 pi]) als Sweep-Nurbs (gelb) dargestellt. Da die Wurzel in Gl. 9-30 zwei Ergebnise liefert erhalten wir natürlich auch 2 Schnittlinien.
Der Ausdruck unter der Wurzel ist aber auch ein Problem, ab einem bestimmten Wert für a wird er negativ und die Wurzel ist nicht mehr reell.
Wir setzen den Ausdruck unter der Wurzel aus Gl. 9-25 gleich Null.
|
|
9-30 |
Wir lösen Gl. 9-30 nach a auf.
|
a = R1 - R2 sin(u2) |
9-31 |
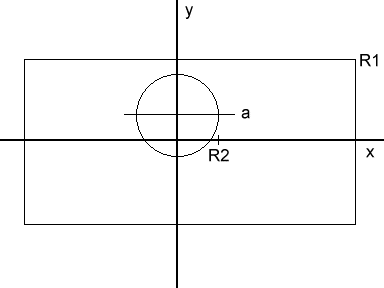
Abb. 14
Im ungünstigsten Fall gilt.
|
|
9-32 |
So gilt für Abb. 14 a < R1 - R2. Bei a = R1 - R2 berührt der kleine Zylinder die Oberkante des großen Zylinders.
Wenn a > R1 - R2 (siehe Abb. 15) gibt es nur noch eine Schnittlinie, bei a > R1 + R2 berührten sich die beiden Zylinder nicht mehr.
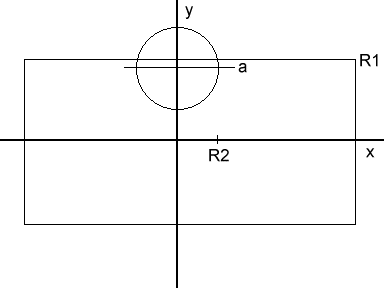
Abb. 15
Bei diesem Modell beschränken wir uns aber auf die Bedingung a < R1 - R2, d.h. der kleine Zylinder wird komplett vom großen Zylinder umschlossen.
| [zurück] | [Inhaltsverzeichnis] | [vor] |