3. Polynominale Knoten
|
[zurück] | 3. Polynominale Knoten |
[vor] | |
Abb. 32 zeigt Gl. 8-75/76 für t [-1, 1], dargestellt werden 20 Punkte.
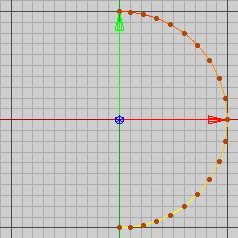
Abb. 32
Abb. 33 zeigt Gl. 8-75/76 für t [-2, 2], dargestellt werden 40 Punkte.
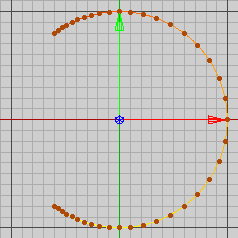
Abb. 33
Abb. 34 zeigt Gl. 8-75/76 für t [-10, 10], dargestellt werden 100 Punkte.
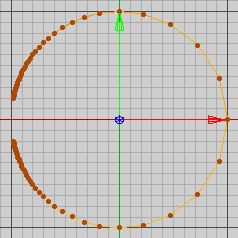
Abb. 34
Abb. 35 zeigt Gl. 8-75/76 für t [-100, 100], dargestellt werden 1000 Punkte.
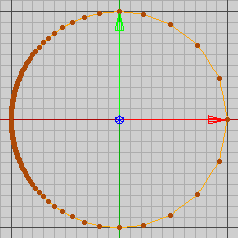
Abb. 35
Es gibt noch einen anderen Weg [15] zu Gleichung 8-75/76 zu kommen. Wir gehen von der impliziten Gleichung des Kreises aus.
|
x2 + y2 - r2 = 0 |
8-78 |
Diese Gleichung zerlegen wir in lineare Faktoren
|
y * y = (r + x)(r - x) |
8-79 |
und stellen sie ein bischen um.
 |
8-80 |
Jetzt fügen wir zusätzlich den Parameter t ein.
 |
8-81 |
|
 |
8-82 |
Wir erhalten ein lineares Gleichungssystem das wir in Matrizenform schreiben.
 |
8-83 |
|
 |
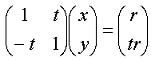8-84 |
Zuerst berechnen wir die Determinante der Matrix.
 |
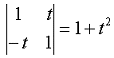8-85 |
Für x und y erhalt man dann.
 |
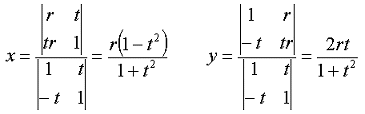8-86 |
Wenn wir den Einheitkreis (r = 1) betrachten erhalten wir das gleiche Ergebnis wie in Gl. 8-75/76.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |