| [zurück] | 3. Polynominale Knoten |
[vor] |
Es gibt eine Möglichkeit die Fourier Knoten aus Kapitel 2 ohne trigonometrische Funktionen darzustellen.
Einen Weg trigonometrische Parametrisierung in eine rationale Parametrisierung umzuwandeln beschreibt David Clark [14]. Ich finde diesen Ansatz interessant und so möchte ich etwas ausführlicher auf die Herleitung eingehen.
Zuerst betrachten wir die Kreisfunktion (siehe Gl. 8-4/5), den Parameter t tauschen wir durch ß aus.
|
x(ß) = cos(ß) |
8-64 |
|
|
y(ß) = sin(ß) |
8-65 |
|
|
für ß [-Pi, Pi] |
8-66 |
Jetzt ersetzen wir ß durch den Ausdruck
|
ß = 2 arctan(t) |
8-67 |
den wir auch ungekehrt schreiben können als
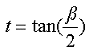 |
8-68 |
Zuerst betrachten wir die Cosinusfunktion die wir nach [19] auch so schreiben können
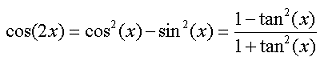 |
8-69 |
Jetzt substituieren wir x durch ß/2 und erhalten
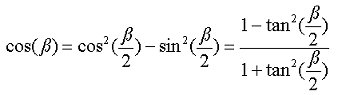 |
8-70 |
In Gl. 8-70 setzten wir jetzt Gl. 8-68 ein und erhalten die gewünschte Gleichung.
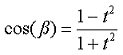 |
8-71 |
Sinngemäß machen wir für die Sinusfunktion Gl. 8-65 das gleiche.
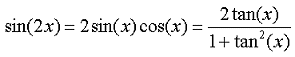 |
8-72 |
|
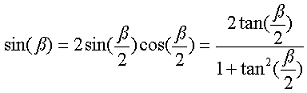 |
8-73 |
|
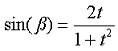 |
8-74 |
Für die Kreisfunktion können wir jetzt als rationale Parametrisierung schreiben.
|
x(t) = (1-t*t)/(1+t*t) |
8-75 |
|
|
y(t) = 2*t/(1+t*t) |
8-76 |
|
|
für t [R] |
8-77 |
Zum besseren Verständnis probieren wir die Gleichungen einfach in Cinema aus. Dazu brauchen wir kein Plugin, wir kopieren sie einfach in das Formel-Spline. Der Wertebereich von t ist entscheidend für das Aussehen des Bildes. Damit die Verteilung der Punkte zu erkennen ist habe ich von Cinema einfach ein Screencopy gemacht.
| [zurück] | [Inhaltsverzeichnis] | [vor] |