[zurück]

Spatprodukt

[vor]

Unter dem Spatprodukt oder Spatvolumen versteht man das Skalarprodukt des aus den Vektoren und gebildeten Vektorproduktes mit dem Vektor.

Die Reihenfolge der Vektoren ist wichtig für das Ergebnis. Bei einer zyklischen Vertauschung der drei Vektoren, und ändert sich das Spatvolumen nicht.

Das Vertauschen zweier Vektoren bewirkt einen Vorzeichenwechsel.

Die Formel zur Berechnung des Spatproduktes läßt sich aus den Formeln zur Berechnung des Skalarproduktes und des Vektorproduktes herleiten. Wir verzichten auf Details und benutzen die Determinantenschreibweise.

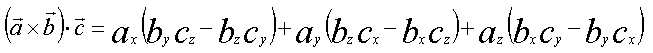
Diese Formel können wir in einer XGroup zusammenfassen.

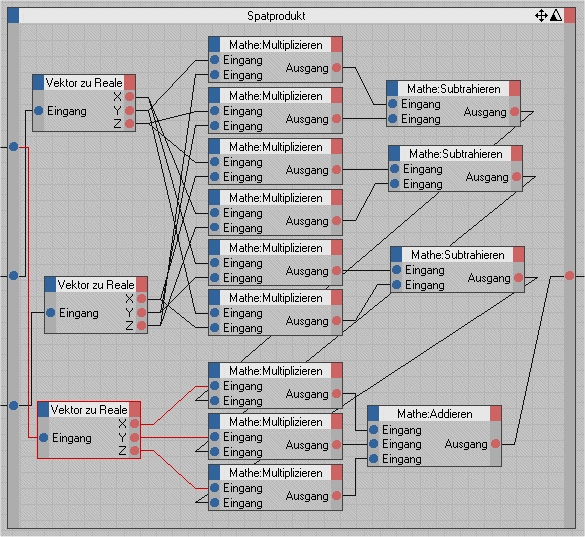
So viele Nodes sind sehr unübersichtlich zumal die Verbindungen nicht editierbar sind und Cinema nicht über eine vernünftige Autoroute Funktion verfügt. Um die ganze Sache etwas übersichtlicher zu gestalten können wir einige Nodes in einem Formelnode zusammenfassen. Am besten die Formel zuerst mit einem Textverarbeitungsprogramm schreiben und dann kopieren.

$1*($5*$9-$6*$8)+$2*($6*$7-$4*$9)+$3*($4*$8-$5*$7)

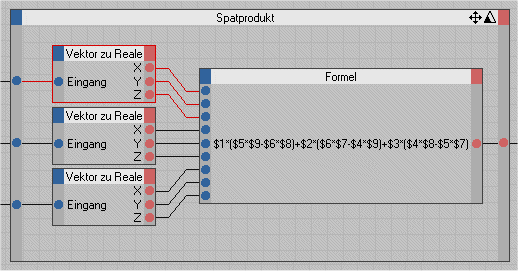
Wir können natürlich auch die vorher definierten XGroups Skalarprodukt und Vektorprodukt benutzen.

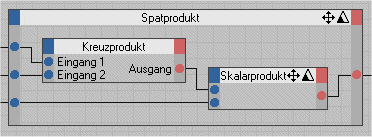
Was bedeutet das Spatprodukt? Das Spatprodukt ist eine Zahl, deren Betrag gleich dem Volumen des von den Vektoren , und aufgespannten Parallelepipeds ist.
Aber wozu können wir das Spatprodukt gebrauchen?
Wir können damit überprüfen ob die drei Vektoren in einer Ebene liegen bzw. linear abhängig sind denn dann ist das Spatprodukt Null.

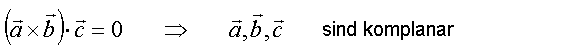
Ist das Spatprodukt positiv dann bilden die Vektoren , und ein rechthändiges System, sonst ist es negativ.

Und zum Schluss noch ein Beispiel.

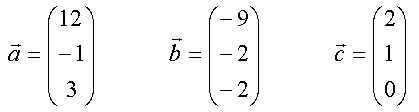
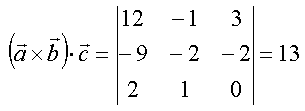
[zurück]

[Inhaltsverzeichnis XPressostoffe]

[vor]