[zurück]

Vektorprodukt

[vor]

Beim Vektor- oder Kreuzprodukt werden zwei Vektoren so multipliziert das das Ergebnis ein Vektor ist. Das Vektorprodukt wird nach folgender Formel berechnet.

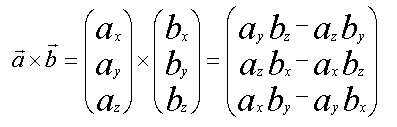
Mit Hilfe der Einheitsvektoren können wir das Vektorprodukt auch in Form einer Determinante schreiben.

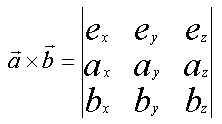
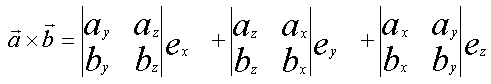
Diese Formel können wir in einer XGroup zusammenfassen.

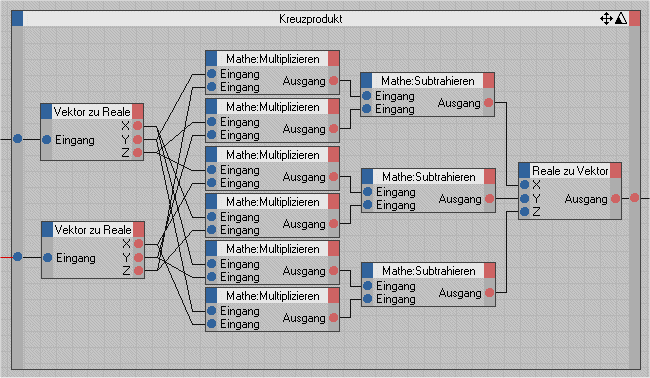
Das Kreuzprodukt ist in Cinema schon definiert, das war also nur eine kleine Übung.

Das Kreuzprodukt ist ein Vektor dessen Betrag der Fläche des von den beiden Vektorenund aufgespannten Parallelogramms entspricht. Seine Richtung entspricht der Flächennormale des aufgespannten Parallelogramms, d.h. er steht senkrecht (orthogonal) zu den beiden Ausgangsvektoren.

Beim Kreuzprodukt ist es anders als beim Skalarprodukt nicht egal in welcher Reihenfolge die Vektoren multipliziert werden. Wird die Reihenfolge geändert, ändert sich das Vorzeichen bzw. der Vektor zeigt in die entgegengesetzte Richtung.

Wenn das Kreuzprodukt Null ist dann sind die beiden Vektorenund kollinear.

Und zum Schluss noch ein Beispiel.

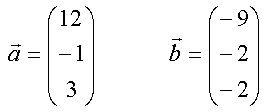
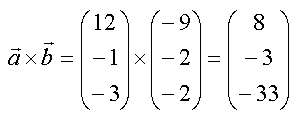
[zurück]

[Inhaltsverzeichnis XPressostoffe]

[vor]