Aufgabe 69
|
[zurück] | Aufgabe 69 |
[vor] | |
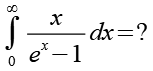(Gl. 1)
Betrachten wir zuerst nur die Funktion f(x).
(Gl. 2)
Zähler und Nenner multiplizieren wit mit e-x.
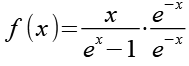(Gl. 3)
(Gl. 4)
Es gilt.
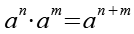(Gl. 5)
Mit Hilfe von Gl. 5 erhalten wir aus Gl. 4.
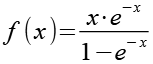(Gl. 6)
Für die geometrische Reihe gilt.
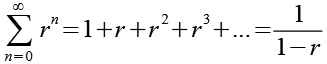(Gl. 7)
mit
(Gl. 8)
Bei der geometrische Reihe ersetzen wir r durch e-x.
(Gl. 9)
Gl. 9 setzen wir in Gl. 7 ein. Gl. 10 kommt Gl. 6 schon recht nahe.
(Gl. 10)
Wir multiplizieren beide Seiten mit x e-x.
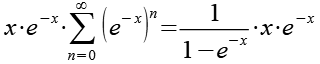(Gl. 11)
(Gl. 12)
Es gilt.
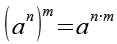(Gl. 13)
Mit Hilfe von Gl. 13 erhalten wir aus Gl. 12.
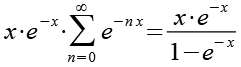(Gl. 14)
Es gilt.
(Gl. 15)
Mit Hilfe von Gl. 15 erhalten wir aus Gl. 14.
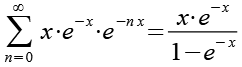(Gl. 16)
Es gilt.
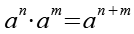(Gl. 5)
Mit Hilfe von Gl. 5 erhalten wir aus Gl. 16.
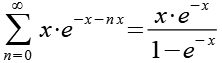(Gl. 17)
Im Exponenten können wir x ausklammern.
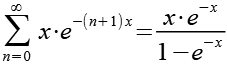(Gl. 18)
Gl. 18 setzen wir in Gl. 2 bzw. Gl. 6 ein.
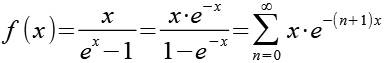(Gl. 19)
Gl. 19 setzen wir in Gl. 1 ein.
(Gl. 20)
Integral und Summenfunktion können wir vertauschen.
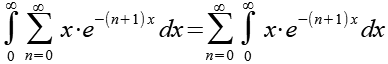(Gl. 21)
Im nächsten Schritt lösen wir das Integral auf der rechten Seite von Gl. 21 (siehe Anhang 1).
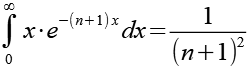(Gl. 22)
Gl. 22 setzen wir in Gl. 21 ein.
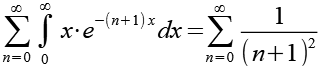(Gl. 23)
Wir berechnen die ersten Glieder der Summenfunktion.
(Gl. 24)
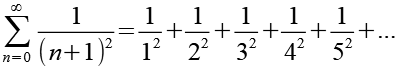(Gl. 25)
Wir ersetzen n+1 durch k.
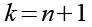(Gl. 26)
Für n=0 folgt aus Gl. 26.
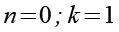(Gl. 27)
Mit der Laufvariablen k erhalten wir so aus Gl. 25.
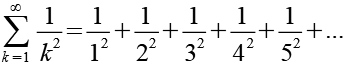(Gl. 28)
Für die Lösung des Basler Problems gilt (siehe Anhang 7).
(Gl. 29)
Mit Hilfe von Gl. 29 erhalten wir die Lösung von Gl. 1.
(Gl. 30)
Zum Schluß noch einmal alle wichtigen Rechenschritte nebeneinander.
(Gl. 31)
Anhang 1
Die Lösung des Integrals aus Gl. 21.
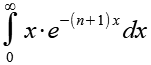(Gl. 32)
Für die partielle Integration gilt.
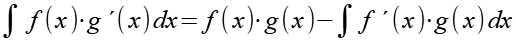(Gl. 33)
Für f(x) und f´(x) erhalten wir aus Gl. 32.
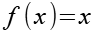(Gl. 34)
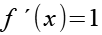(Gl. 35)
Für g´(x) und g(x) erhalten wir aus Gl. 32. Zur Berechnung von g(x) siehe Anhang 2.
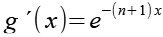(Gl. 36)
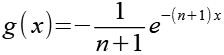(Gl. 37)
Wir setzen Gl. 34, Gl. 35, Gl. 36 und Gl. 37 in Gl. 33 ein und erhalten als Lösung von Gl. 32.
(Gl. 38)
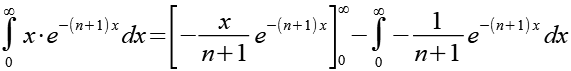(Gl. 39)
Betrachten wir zuerst die eckige Klammer mit den Integrationsgrenzen.
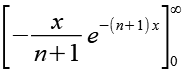(Gl. 40)
Wir betrachten die Aufgabe als Grenzwert und erhalten für x=0 (siehe Anhang 3).
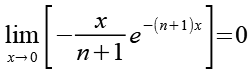(Gl. 41)
Wir betrachten die Aufgabe als Grenzwert und erhalten für x=unendlich (siehe Anhang 4).
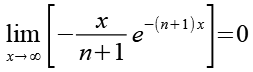(Gl. 42)
Wir setzen das Ergebnis von Gl. 41 und Gl. 42 in Gl. 39 ein.
(Gl. 43)
(Gl. 44)
Es gilt.
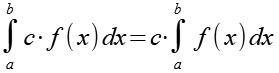(Gl. 45)
Mit Hilfe von Gl. 45 erhalten wir aus Gl. 44.
(Gl. 46)
Für die Lösung des Integrals auf der rechten Seite erhalten wir (siehe Anhang 2).
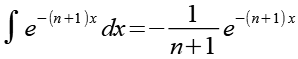(Gl. 47)
Wir setzen Gl. 47 unter Berücksichtigung der Integrationsgrenzen in Gl. 46 ein.
(Gl. 48)
Wir betrachten die eckige Klammer wieder als Grenzwert. Für x=0 erhalten wir (siehe Anhang 5).
(Gl. 49)
Für x=unendlich erhalten wir (siehe Anhang 6).
(Gl. 50)
Wir setzen Gl. 49 und Gl. 50 in Gl. 48 ein.
(Gl. 51)
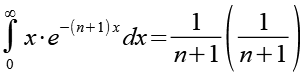(Gl. 52)
(Gl. 53)
Anhang 2
Lösung des Integrals.
(Gl. 54)
Wir substituieren -(n+1)x durch u.
(Gl. 55)
Gl. 55 wird differenziert.
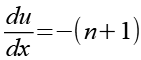(Gl. 56)
Wir lösen Gl. 56 nach dx auf.
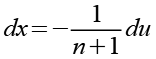(Gl. 57)
Wir setzen Gl. 55 und Gl. 57 in Gl. 54 ein.
(Gl. 58)
Für das Integral der e Funktion gilt.
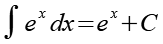(Gl. 59)
Mit Hilfe von Gl. 59 erhalten wir aus Gl. 58.
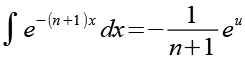(Gl. 60)
Im letzen Schritt setzen wir Gl. 55 in Gl. 60 ein.
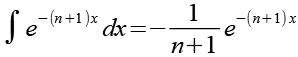(Gl. 61)
Anhang 3
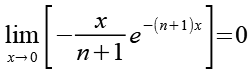(Gl. 41)
Ein Zahlenbeispiel für n=2.
| x | |
|
1 0,1 0,01 0,001 0,0001 0,00001 0,000001 0,0000001 |
-0,0165956894 -0,0246939406 -0,0032348184 -0,0003323348 -0,0000333233 -0,0000033332 -0,0000003333 -0,0000000333 |
Anhang 4
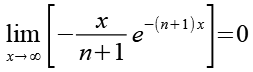(Gl. 42)
Ein Zahlenbeispiel für n=2.
| x | |
|
1 2 3 4 5 6 7 |
-0,0165956894 -0,0016525014 -0,0001234098 -0,0000081922 -0,0000005098 -0,0000000304 -0,0000000017 |
Anhang 5
(Gl. 49)
Es gilt.
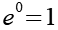(Gl. 62)
Mit Hilfe von Gl. 62 erhalten wir aus Gl. 49.
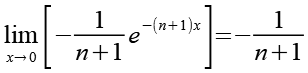(Gl. 63)
Anhang 6
(Gl. 50)
Ein Zahlenbeispiel für n=2.
| x | |
|
1 2 3 4 5 6 7 |
-0,016595689456 -0,000826250725 -0,000041136601 -0,000002048070 -0,000000101967 -0,000000005076 -0,000000000252 |
Anhang 7
(Gl. 29)
| k | Summe |
|
1 10 100 1000 10000 100000 1000000 10000000 100000000 |
1,00000000000 1,54976773117 1,63498390018 1,64393456668 1,64483407185 1,64492406690 1,64493306685 1,64493396685 1,64493405783 |
| pi2/6 | 1,64493406685 |
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |