Aufgabe 57
|
[zurück] | Aufgabe 57 |
[vor] | |
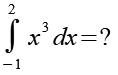(Gl. 1)
Dieses Integral konventionell zu lösen ist natürlich trivial, siehe siehe Anhang.
Hier wollen wir das Integral aber über die Riemann Summe lösen, für die Riemann Summe gilt
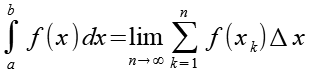(Gl. 2)
mit
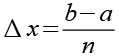(Gl. 3)
und
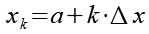(Gl. 4)
Die Integrationsgrenzen sind in unserem Beispiel.
(Gl. 5)
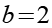(Gl. 6)
Die Funktion.
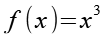(Gl. 7)
Die Formel für die Riemann Summen entwickeln wir Schrittweise, wir fangen mit Delta x an und setzen Gl. 5 und Gl. 6 in Gl. 3 ein.
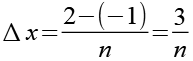(Gl. 8)
Wir setzen Gl. 5 und Gl. 8 in Gl. 4 ein.
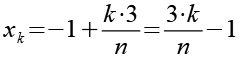(Gl. 9)
Wir setzen Gl. 9 in Gl. 7 ein.
(Gl. 10)
Es gilt.
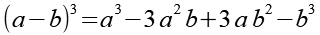(Gl. 11)
Mit Hilfe von Gl. 11 erhalten wir aus Gl. 10.
(Gl. 12)
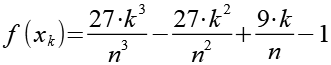(Gl. 13)
Im nächsten Schritt vereinen wir Gl. 13 und Gl. 8.
(Gl. 14)
Die Klammern werden ausmultipliziert.
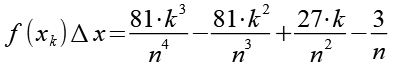(Gl. 15)
Wir erweitern Gl. 15 um die Summenfunktion.
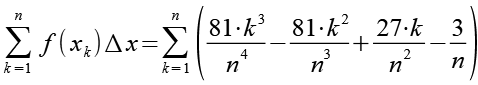(Gl. 16)
Es gilt.
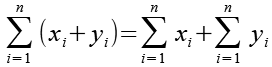(Gl. 17)
Mit Hilfe von Gl. 17 erhalten wir aus Gl. 16.
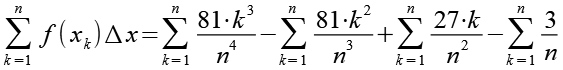(Gl. 18)
Es gilt.
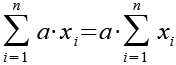(Gl. 19)
Mit Hilfe von Gl. 19 erhalten wir aus Gl. 18.
(Gl. 20)
Für die Summenfunktionen gilt.
(Gl. 21)
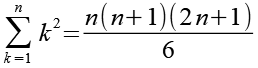(Gl. 22)
(Gl. 23)
(Gl. 24)
Wir setzen Gl. 21, Gl. 22, Gl. 23 und Gl. 24 in Gl. 20 ein.
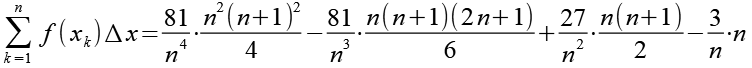(Gl. 25)
Die Nenner werden etwas umgestellt, wir können einmal n kürzen.
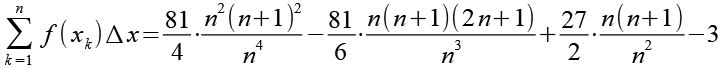(Gl. 26)
n3 ersetzen wir durch n ⋅ n ⋅ n.
(Gl. 27)
(Gl. 28)
Die Brüche ersetzen wir durch ein Produkt aus Brüchen.
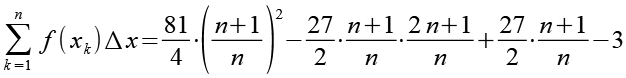(Gl. 29)
Es gilt.
(Gl. 30)
Mit Hilfe von Gl. 30 erhalten wir aus Gl. 29.
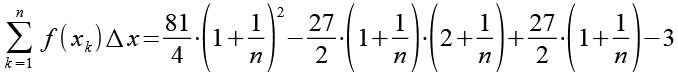(Gl. 31)
Jetzt haben wir alle Teile der Riemann Summe berechnet und können sie zusammenfügen.
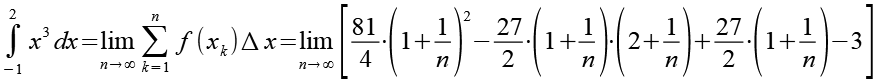(Gl. 32)
Es gilt.
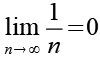(Gl. 33)
Mit Hilfe von Gl. 33 erhalten wir aus Gl. 32.
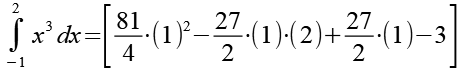(Gl. 34)
(Gl. 35)
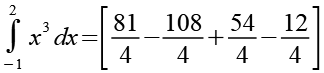(Gl. 36)
Das Ergebnis.
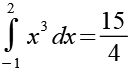(Gl. 37)
Anhang
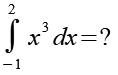(Gl. 1)
Für das Integral der Potenzfunktion gilt.
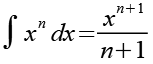(Gl. 38)
Mit Hilfe von Gl. 38 erhalten wir aus Gl. 1.
(Gl. 39)
(Gl. 40)
Das Ergebnis.
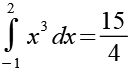(Gl. 37)
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |