[zurück]

Aufgabe 55

[vor]

      (Gl. 1)

Wir bezeichnen den Grenzwert mit L.

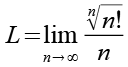      (Gl. 2)

Es gilt.

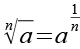      (Gl. 57)

Mit Hilfe von Gl. 57 erhalten wir aus Gl. 2.

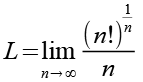      (Gl. 3)

Wir wenden auf beiden Seiten den Logarithmus an.

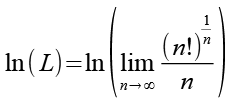      (Gl. 4)

Die Reihenfolge von Logarithmus und Grenzwert können wir vertauschen.

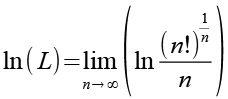      (Gl. 5)

Es gilt.

      (Gl. 6)

Mit Hilfe von Gl. 6 erhalten wir aus Gl. 5.

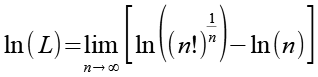      (Gl. 7)

Es gilt.

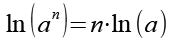      (Gl. 8)

Mit Hilfe von Gl. 8 erhalten wir aus Gl. 7.

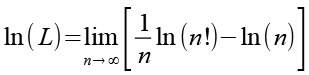      (Gl. 9)

Für die Fakultät gilt.

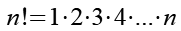      (Gl. 10)

Es gilt.

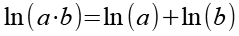      (Gl. 11)

Für ln(n!) können wir mit Hilfe von Gl. 10 und Gl. 11 auch schreiben.

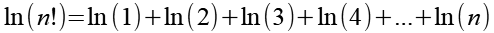      (Gl. 12)

Gl. 12 können wir auch als Summenfunktion formulieren.

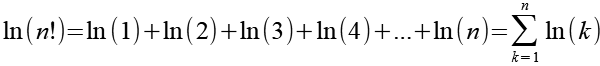      (Gl. 13)

Gl. 13 können wir jetzt in Gl. 9 einsetzen.

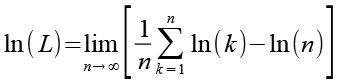      (Gl. 14)

Jetzt wäre es sinnvoll auch ln(n) durch eine Summenfunktion auszudrücken, dazu multiplizieren wir ln(n) mit n/n.

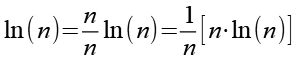      (Gl. 15)

Für die Summenfunktion erhalten wir.

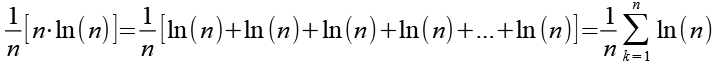      (Gl. 16)

ln(n) als Summenfunktion.

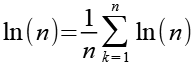      (Gl. 17)

Wir setzen Gl. 17 in Gl. 14 ein.

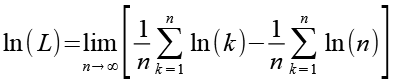      (Gl. 18)

Es gilt.

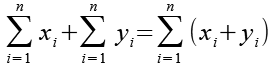      (Gl. 19)

Mit Hilfe von Gl. 19 erhalten wir aus Gl. 18.

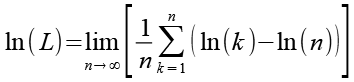      (Gl. 20)

Es gilt.

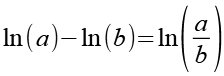      (Gl. 21)

Mit Hilfe von Gl. 21 erhalten wir aus Gl. 20.

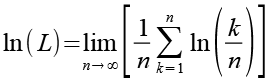      (Gl. 22)

Für die weitere Berechnung nutzen wir die Riemann Summe, es gilt.

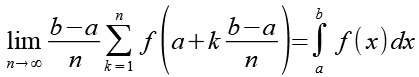      (Gl. 23)

Als Integrationsgrenzen setzen wir a=0 und b=1 ein.

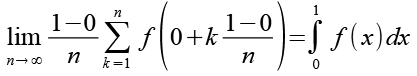      (Gl. 24)

Das Ergbnis entspricht der rechten Seite von Gl. 22.

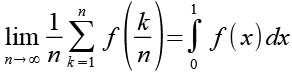      (Gl. 25)

Wir können Gl. 25 in Gl. 22 einsetzen.

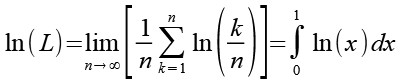      (Gl. 26)

Für das Integral gilt (siehe Anhang 1).

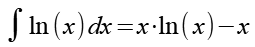      (Gl. 27)

Wir setzen die Integrationsgrenzen ein.

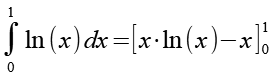      (Gl. 28)

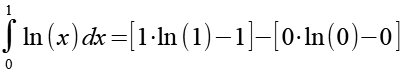      (Gl. 29)

ln(0) ist nicht definiert, wir berechnen diesen Ausdruck über einen Grenzwert (siehe Anhang 2).

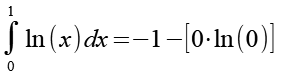      (Gl. 30)

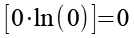      (Gl. 31)

Mit Hilfe von Gl. 31 erhalten wir aus Gl. 30.

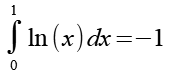      (Gl. 32)

Gl. 32 setzen wir in Gl. 26 ein.

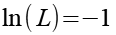      (Gl. 33)

Auf beiden Seiten wenden wir die Exponentialfunktion an.

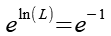      (Gl. 34)

Auf der linken Seite heben sich Logarithmus und Exponentialfunktion auf.

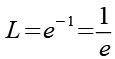      (Gl. 35)

Das Ergebnis.

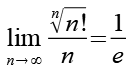      (Gl. 36)

Anhang 1

Für die Berechnung des Integrals nutzen wir die partielle Integration, es gilt

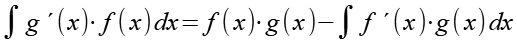      (Gl. 37)

Das Integral erweitern wir um den Faktor 1 und damit um die Funktion g´(x).

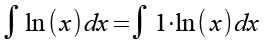      (Gl. 38)

f(x) und seine Ableitung.

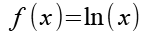      (Gl. 39)

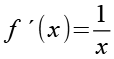      (Gl. 40)

g(x) und seine Ableitung.

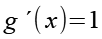      (Gl. 41)

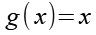      (Gl. 42)

Wir setzen Gl. 39, Gl. 40, Gl. 41 und Gl. 42 in Gl. 37 ein.

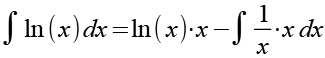      (Gl. 43)

Auf der rechten Seite können wir x kürzen.

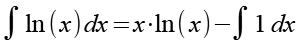      (Gl. 44)

Es gilt.

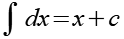      (Gl. 45)

Mit Hilfe von Gl. 45 erhalten wir das Ergebnis für das Integral von ln(x).

      (Gl. 46)

Anhang 2

ln(0) ist nicht definiert, für die Berechnung nutzen wir den Grenzwert.

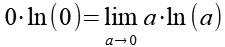      (Gl. 47)

Gl. 47 stellen wir etwas um.

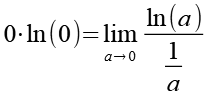      (Gl. 48)

Wir nutzen die Regel von de L’Hospital.

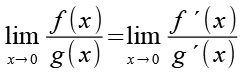      (Gl. 49)

f(x) und seine Ableitung.

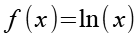      (Gl. 50)

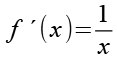      (Gl. 51)

g(x) und seine Ableitung (siehe Anhang 3).

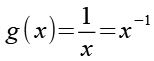      (Gl. 52)

      (Gl. 53)

Wir setzen Gl. 50, Gl. 51, Gl. 52 und Gl. 53 in Gl. 49 ein.

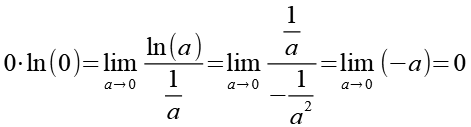      (Gl. 54)

Anhang 3

Für die Ableitung der Potenzfunktion gilt.

      (Gl. 55)

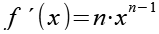      (Gl. 56)

Anhang 4

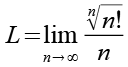      (Gl. 2)

[zurück]

[Inhaltsverzeichnis]

[vor]