| [zurück] | 3.166. Gewellter Torus II |
[vor] |
Der Gewellte Torus II wird durch folgende Gleichungen dargestellt.
|
x = (R1 + R2 cos(n u) + r cos(v)) cos(u) |
3-560 |
|
|
y = r sin(v) |
3-561 |
|
|
z = (R1 + R2 cos(n u) + r cos(v)) sin(u) |
3-562 |
Als Basis für den Gewellten Torus II dienten die Gleichungen 8-125, 8-126, 8-123 aus meinem Knoten Tutorial.
Die Konstanten R1, R2, r und n bestimmen das Aussehen der Figur.
Zur Darstellung der Fläche können die beiden Parameter u und v zum Beispiel folgende Werte (Definitionsbereich) annehmen.
|
u ist Element aus der Zahlenmenge [0, 2 pi] |
||
|
v ist Element aus der Zahlenmenge [0, 2 pi] |
Da es sich beim Gewellter Torus II um eine geschlossene Figur handelt muss der Definitionsbereich exakt
eingehalten werden, er kann beim Plugin nicht verändert werden.
Das Plugin erzeugt ein optimiertes Mesh ohne doppelte Punkte und nichtverbundene Polygone.
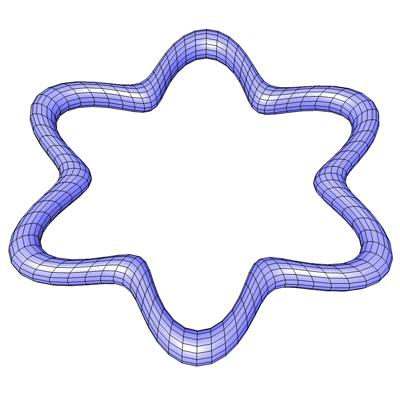
Abb. 243
Die Figur kann auf der nächsten Seite mit einem Java-Applet von allen Seiten betrachtet und gedreht werden.
Abb. 244 zeigt die Draufsicht, die Querschnitte der einzelnen Segmente sind auf den Koordinatenursprung ausgerichtet.
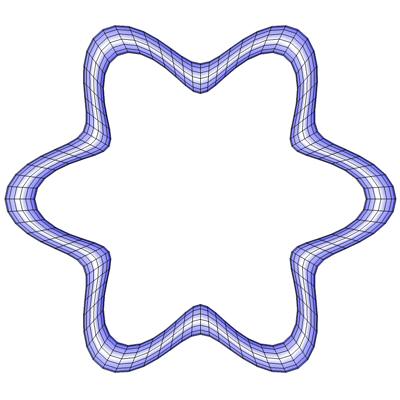
Abb. 244
| [zurück] | [Inhaltsverzeichnis] | [vor] |