| [zurück] | 4. Torus Knoten |
[vor] |
Eine Animation sagt mehr als 1000 Worte, deshalb spare ich mir längere Erklärungen zum Torusknoten. Die Animation besteht aus 100 Frames (320*240) und wurde mit Animation Shop 3 von Jasc Software in ein Gif umgewandelt. Die Gif Datei ist nur erstaunliche 19 KB gross.
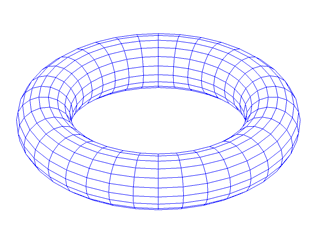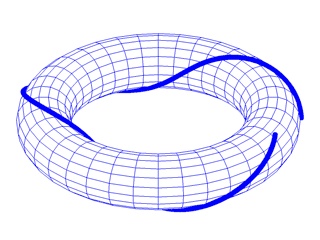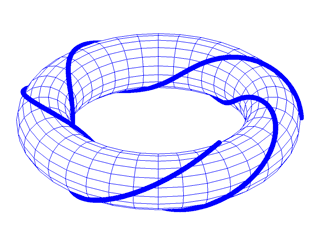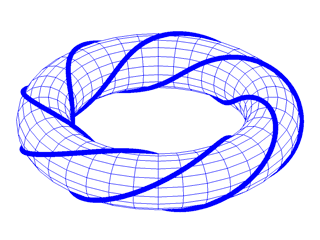
Abb. 43
Dieses Beispiel zeigt einen Torusknoten (7,3), er windet sich dreimal um den Torus und überstreicht ihn dabei 7 mal.
Der Torusknoten wird durch folgende Gleichungen erzeugt [21, 22, 26].
|
x(t) = (R + r * cos(p * t)) * cos(q * t) |
8-118 |
|
|
y(t) = (R + r * cos(p * t)) * sin(q * t) |
8-119 |
|
|
z(t) = r * sin(p * t) |
8-120 |
Die Kontanten R und r bestimmen Form und Größe des Torus, die Konstanten p und q bestimmen die Art des Knotens, in unserem Beispiel ist R=100, r=25, p=7 und q=3. Für einen korrekten Torusknoten dürfen p und q keine gemeinsamen Teiler haben.
Jetzt versuchen wir einmal die Formeln herzuleiten. Wir gehen wieder von der Kreisfunktion Gl. 8-4/6 aus (y und z Achse wurden vertauscht). In Abb. 44 zeigt das linke Bild die Draufsicht, das rechte Bild die isometrische Darstellung.
|
x(t) = 100 * cos(t) |
8-121 |
|
|
y(t) = 100 * sin(t) |
8-122 |
|
|
z(t) = 0 |
8-123 |

Abb. 44
Die Kreisfunktion erweitern wir um eine Schwingung in z Richtung mit p=7 Perioden und einer Amplitude von r=25.
|
x(t) = 100 * cos(t) |
8-121 |
|
|
y(t) = 100 * sin(t) |
8-122 |
|
|
z(t) = 25 * sin(7 * t) |
8-124 |

Abb. 45
Jetzt nehmen wir wieder die Kreisfunktion Gl. 8-121/123 und modulieren den Radius mit einer Cosinusfunktion. Als Amplitude für die Modulation verwenden wir wieder r=25 und wie bei Gl. 8-124 7 Perioden. Das Ergebnis sehen wir in Abb. 46.
|
x(t) = (100 + 25 * cos(7 * t)) * cos(t) |
8-125 |
|
|
y(t) = (100 + 25 * cos(7 * t)) * sin(t) |
8-126 |
|
|
z(t) = 0 |
8-123 |

Abb. 46
Jetzt kombinieren wir die Gleichungen 8-125/126 und 8-124 und erhalten einen Torusknoten (7,1).
|
x(t) = (100 + 25 * cos(7 * t)) * cos(t) |
8-125 |
|
|
y(t) = (100 + 25 * cos(7 * t)) * sin(t) |
8-126 |
|
|
z(t) = 25 * sin(7 * t) |
8-124 |

Abb. 47
Damit sich der Torusknoten 3 mal um den Torus windet müssen wir nur noch die Konstante q=3 einfügen und erhalten so den gewünschten Torusknoten (7,3).
|
x(t) = (100 + 25 * cos(7 * t)) * cos(3 * t) |
8-127 |
|
|
y(t) = (100 + 25 * cos(7 * t)) * sin(3 * t) |
8-128 |
|
|
z(t) = 25 * sin(7 * t) |
8-129 |

Abb. 48
Der Torusknoten kommt viel besser zur Geltung wenn wir den Torus mitzeichnen.

Abb. 49
Das Plugin zur Erzeugung der Torusknoten (für Cinema Version 7 und 8) kann auf der Download Seite runtergeladen werden.
| [zurück] | [Inhaltsverzeichnis] | [vor] |