| [zurück] | 3.149. Versiera der Agnesi Zylinder |
[vor] |
Der Versiera der Agnesi Zylinder wird durch folgende Gleichungen dargestellt.
|
x = (R + 2 a/(1 + v2)) cos(u) |
3-486 |
|
|
y = 2 a v |
3-487 |
|
|
z = (R + 2 a/(1 + v2)) sin(u) |
3-488 |
Die Konstanten R und a bestimmen das Aussehen der Figur.
Zur Darstellung der Fläche können die beiden Parameter u und v zum Beispiel folgende Werte (Definitionsbereich) annehmen.
|
u ist Element aus der Zahlenmenge [-pi, pi] |
||
|
v ist Element aus der Zahlenmenge [-3, 3] |
Beim Versiera der Agnesi Zylinder handelt es sich um eine halboffene Figur, der Definitionsbereich von v kann daher beim Plugin verändert werden.
Das Plugin erzeugt ein optimiertes Mesh ohne doppelte Punkte und nichtverbundene Polygone.
Abb. 217
Die Figur kann auf der nächsten Seite mit einem Java-Applet von allen Seiten betrachtet und gedreht werden.
In die Figur läßt sich ein Torus bündig einpassen.
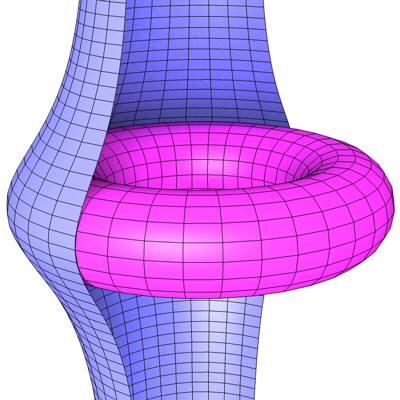
Abb. 218
Die Versiera der Agnesi (Abb. 219) wird durch folgende Gleichungen dargestellt.
|
x = 2 a t |
3-489 |
|
|
y = 2 a/(1 + t2) |
3-490 |

Abb. 219
Weitere Informationen zur Versiera der Agnesi gibt es in meinem Formelspline Tutorial.
| [zurück] | [Inhaltsverzeichnis] | [vor] |