| [zurück] | 3.9. Möbius Band |
[vor] |
Das Möbius Band [6,7,11] wurde nach dem deutschen Mathematiker und Astronomen August Ferdinand Möbius (1790-1868) benannt. Ein Möbius Band sollte sich jeder Interessierte einmal selber herstellen. Einfach einen langen schmalen Papierstreifen nehmen und die Enden (um 180° verdreht) zusammenkleben.
Dieses Band hat nun einige merkwürdige Eigenschaften. Es besitzt nur eine einzige Seite obwohl es eigentlich nicht so aussieht. Wer es nicht glaubt sollte einmal versuchen eine Seite des Bandes anzumalen oder auf einer Seite entlang des Bandes eine Linie zu zeichnen.
Das Band besitzt auch nur eine Kante. Wer es nicht glaubt sollte einmal versuchen das Band mit einer Schere längs durchzuschneiden. Es wird nicht gelingen, denn ein Band mit einer Kante bleibt auch nach dem Durchschneiden ein einziges Band. Noch verblüffender wird es wenn wir dieses Band noch einmal versuchen durchzuschneiden.
Das Möbius Band wird durch folgende Gleichungen dargestellt.
|
x = [R + s cos(t/2)] cos(t) |
3-39 |
|
|
y = [R + s cos(t/2)] sin(t) |
3-40 |
|
|
z = s sin(t/2) |
3-41 |
Die Konstante R bestimmt den Radius des Bandes. Beim Parameter s = 0 erhalten wir einen Kreis mit dem Radius R und der Höhe z = 0.
Die Konstante w bestimmt die Breite des Bandes.
Zur Darstellung der Fläche müssen die beiden Parameter s und t folgende Werte (Definitionsbereich) annehmen.
|
s ist Element aus der Zahlenmenge [-w, w] |
||
|
t ist Element aus der Zahlenmenge [0, 2 pi] |
Da es sich beim Möbius Band um eine geschlossene Figur handelt muß der Definitionsbereich für den Parameter t exakt eingehalten werden.
Das Plugin erzeugt ein optimiertes Mesh ohne doppelte Punkte und nichtverbundene Polygone.
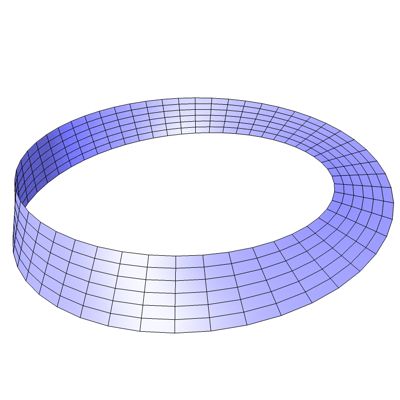
Abb. 13
Die Figur kann auf der nächsten Seite mit einem Java-Applet von allen Seiten betrachtet und gedreht werden.
| [zurück] | [Inhaltsverzeichnis] | [vor] |