| [zurück] | 3.8. Klein Bottle |
[vor] |
Die sogenannte Kleinsche Flasche [6,9,10,11,19] wurde nach dem Mathematiker Felix Klein benannt. Sie ist eine dreidimensionale Erweiterung des Möbius Bandes. Bildlich vorgestellt ist die Kleinsche Flasche ein Schlauch, der über die vierte Dimension so verdreht und in sich selbst gestülpt wurde, daß ein Gegenstand, der ihn durchwandert, seine Reise seitenverkehrt beendet.
Die Kleinsche Flasche wird durch folgende Gleichungen dargestellt. Um die Formeln etwas übersichtlicher zu halten benutzen wir die Konstante r.
|
r = 4 (1 - cos(u)/2) |
3-30 |
Zur Darstellung der Klein Bottle sind unterschiedliche Gleichungen für Teile des Definitionsbereiches von u erforderlich.
|
0 <= u < pi |
3-31 |
|
|
x = a cos(u) (1 + sin(u)) + r cos(u) cos(v) |
3-32 |
|
|
y = b sin(u) + r sin(u) cos(v) |
3-33 |
|
|
z = r sin(v) |
3-34 |
|
pi < u <= 2pi |
3-35 |
|
|
x = a cos(u) (1 + sin(u)) + r cos(v + pi) |
3-36 |
|
|
y = b sin(u) |
3-37 |
|
|
z = r sin(v) |
3-38 |
Die Konstanten a und b bestimmen das Aussehen der Figur.
Zur Darstellung der Fläche müssen die beiden Parameter u und v folgende Werte (Definitionsbereich) annehmen.
|
u ist Element aus der Zahlenmenge [0, 2 pi] |
||
|
v ist Element aus der Zahlenmenge [0, 2 pi] |
Da es sich bei der Klein Bottle um eine geschlossene Figur handelt muß der Definitionsbereich exakt eingehalten werden, er kann deshalb beim Plugin auch nicht verändert werden.
Das Plugin erzeugt ein optimiertes Mesh ohne doppelte Punkte und nichtverbundene Polygone.
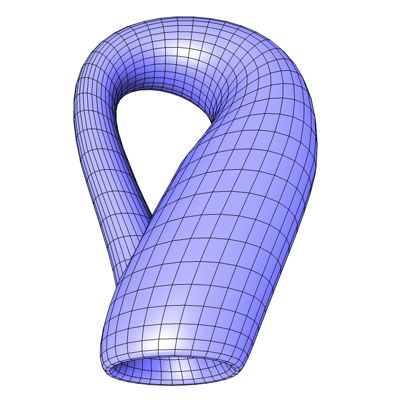
Abb. 12
Die Figur kann auf der nächsten Seite mit einem Java-Applet von allen Seiten betrachtet und gedreht werden.
| [zurück] | [Inhaltsverzeichnis] | [vor] |