| [zurück] | Apple II Surface |
[vor] |
Jetzt versuchen wir einmal herauszufinden wie die Gleichungen für die Apple II Surface zustande gekommen sind. Wir gehen dabei von einem einfachen Torus aus dessen Parameter (R und r) wir an dem Apfel anpassen. Wir erhalten dann folgende Gleichungen.
|
x = cos(u) (5.0 + 4.8 cos(v)) |
3-293 |
|
|
y = sin(u) (5.0 + 4.8 cos(v)) |
3-294 |
|
|
z = 6 sin(v) |
3-295 |
Dieser Torus ist in Abb. 111 dargestellt. Das mittlere Bild zeigt die Draufsicht, das rechte Bild die Seitenansicht des aufgeschnittenen Objektes.
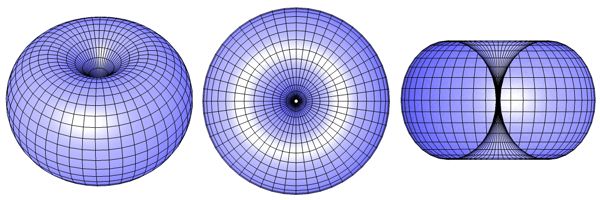
Abb. 111
Dieser Torus hat noch nicht allzuviel mit einem Apfel zu tun. Der Querschnitt ist etwas asymmetrisch und zeigt eine Ellipse. Jetzt addieren wir den Ausdruck 2 cos(v) zu Gleichung 3-295.
|
x = cos(u) (5.0 + 4.8 cos(v)) |
3-293 |
|
|
y = sin(u) (5.0 + 4.8 cos(v)) |
3-294 |
|
|
z = 6 sin(v) + 2 cos(v) |
3-296 |
Die Kontur des Apfels wird oben etwas breiter und unten etwas schmaler.

Abb. 112
Als nächstes machen wir den Umfang des Apfels etwas eckiger indem wird den Ausdruck 0.25 cos(5 u) zu Gl. 3-294 addieren.
|
x = cos(u) (5.0 + 4.8 cos(v)) |
3-293 |
|
|
y = sin(u) (5.0 + 4.8 cos(v)) + 0.25 cos(5 u) |
3-297 |
|
|
z = 6 sin(v) + 2 cos(v) |
3-296 |
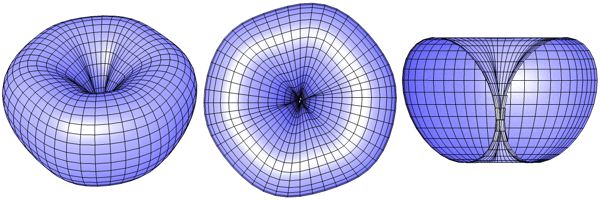
Abb. 113
Jetzt wird es kompliziert, wir müssen den Stengel des Apfels modellieren. Dazu addieren wir den Ausdruck -log(1 - v 0.3157) zu Gl. 3-296.
|
x = cos(u) (5.0 + 4.8 cos(v)) |
3-293 |
|
|
y = sin(u) (5.0 + 4.8 cos(v)) + 0.25 cos(5 u) |
3-297 |
|
|
z = -log(1 - v 0.3157) + 6 sin(v) + 2 cos(v) |
3-298 |

Abb. 114
Wie wir sehen ist der Apfel bzw. Torus jetzt in der Mitte geteilt, ein Stengel ist aber noch nicht zu erkennen. Wir erhöhen den Einfluß der log Funktion indem wir sie mit 2.3 mulziplizieren.
|
x = cos(u) (5.0 + 4.8 cos(v)) |
3-293 |
|
|
y = sin(u) (5.0 + 4.8 cos(v)) + 0.25 cos(5 u) |
3-297 |
|
|
z = -2.3 log(1 - v 0.3157) + 6 sin(v) + 2 cos(v) |
3-299 |
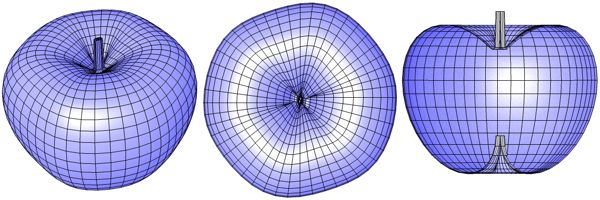
Abb. 115
Jetzt haben wir einen Stengel. Aber warum hat die log Funktion diesen Einfluß auf den Apfel? Um das herauszufinden schauen wir uns diese Funktion etwas genauer an. Dazu zeichnen wir die Funktion in ein x,y Koordinatenkreuz.
| [zurück] | [Inhaltsverzeichnis] | [vor] |