| [zurück] | 8. Die Bernoulli-Zahlen |
[vor] |
Die Bernoulli-Zahlen [] wurden nach dem Schweizer Mathematiker Jakob Bernoulli (1654 - 1705) benannt, sie können mit folgender Formel berechnet werden (Bernoulli-Formel.py, Bernoulli-Formel-Dezimal.py).
![]()
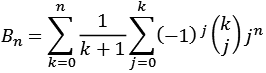
Mit Hilfe der Binominalkoeffizienten läßt sich die Formel umstellen.
![]()
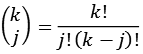
![]()
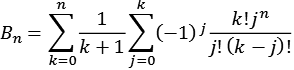
Die folgende Tabelle zeigt die Bernoulli-Zahlen bis n = 50 (Bernoulli-Zahlen.py).
| n | Zähler | Nenner | Bn |
| 0 | 1 | 1 | 1,0000000000 |
| 1 | -1 | 2 | -0,5000000000 |
| 2 | 1 | 6 | 0,1666666667 |
| 3 | 0 | ||
| 4 | -1 | 30 | -0,0333333333 |
| 5 | 0 | ||
| 6 | 1 | 42 | 0,0238095238 |
| 7 | 0 | ||
| 8 | -1 | 30 | -0,0333333333 |
| 9 | 0 | ||
| 10 | 5 | 66 | 0,0757575758 |
| 11 | 0 | ||
| 12 | -691 | 2730 | -0,2531135531 |
| 13 | 0 | ||
| 14 | 7 | 6 | 1,1666666667 |
| 15 | 0 | ||
| 16 | -3617 | 510 | -7,0921568627 |
| 17 | 0 | ||
| 18 | 43867 | 798 | 54,9711779449 |
| 19 | 0 | ||
| 20 | -174611 | 330 | -529,1242424242 |
| 21 | 0 | ||
| 22 | 854513 | 138 | 6192,1231884058 |
| 23 | 0 | ||
| 24 | -236364091 | 2730 | -86580,2531135531 |
| 25 | 0 | ||
| 26 | 8553103 | 6 | 1425517,1666666667 |
| 27 | 0 | ||
| 28 | -23749461029 | 870 | -27298231,0678160920 |
| 29 | 0 | ||
| 30 | 8615841276005 | 14322 | 601580873,9006423684 |
| 31 | 0 | ||
| 32 | -7709321041217 | 510 | -15116315767,0921568627 |
| 33 | 0 | ||
| 34 | 2577687858367 | 6 | 429614643061,1666666667 |
| 35 | 0 | ||
| 36 | -26315271553053477373 | 1919190 | -13711655205088,3327721591 |
| 37 | 0 | ||
| 38 | 2929993913841559 | 6 | 488332318973593,1666666667 |
| 39 | 0 | ||
| 40 | -261082718496449122051 | 13530 | -19296579341940068,1486326681 |
| 41 | 0 | ||
| 42 | 1520097643918070802691 | 1806 | 841693047573682615,0005537099 |
| 43 | 0 | ||
| 44 | -27833269579301024235023 | 690 | -40338071854059455413,0768115942 |
| 45 | 0 | ||
| 46 | 596451111593912163277961 | 282 | 2115074863808199160560,1453900709 |
| 47 | 0 | ||
| 48 | -5609403368997817686249127547 | 46410 | -120866265222965259346027,3119370825 |
| 49 | 0 | ||
| 50 | 495057205241079648212477525 | 66 | 7500866746076964366855720,0757575758 |
Für die Bernoulli-Zahlen gibt es eine interessante Näherungsformel (Bernoulli-Nahe.py). Ab n = 5 liegt die Abweichung unter 1 %.
![]()
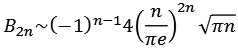
| n | Näherung | B2n | Abweichung |
| 1 | 0,0972178961538 | 0,166666666667 | 41,67 % |
| 2 | -0,0301642470987 | -0,0333333333333 | 9,51 % |
| 3 | 0,0230811240841 | 0,0238095238095 | 3,06 % |
| 4 | -0,032854133474 | -0.0333333333333 | 1,44 % |
| 5 | 0,0750544466199 | 0,0757575757576 | 0,93 % |
| 6 | -0,251300470845 | -0,253113553114 | 0,72 % |
| 7 | 1,15967299377 | 1,16666666667 | 0,60 % |
| 8 | -7,0552115323 | -7,09215686275 | 0,52 % |
| 9 | 54,7170871219 | 54,9711779449 | 0,46 % |
| 10 | -526,923824965 | -529.124242424 | 0,42 % |
| 11 | 6168,71268003 | 6192.12318841 | 0,38 % |
| 12 | -86280,1607365 | -86580.2531136 | 0,35 % |
| 13 | 1420955,71894 | 1425517.16667 | 0,32 % |
| 14 | -27217110,4539 | -27298231.0678 | 0,30 % |
| 15 | 599912195,825 | 601580873.901 | 0,28 % |
| 16 | -15077002848,2 | -15116315767.1 | 0,26 % |
| 17 | 428562985610,0 | 429614643061.0 | 0,24 % |
Ein weitere interessante Eigenschaft der Bernoulli-Zahlen. Addiert man zur Bernoulli-Zahl die Kehrwerte der Primzahlzerlegung des Nenners erhält man immer eine ganze Zahl. Einige Beispiele:
| B2: | 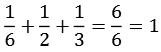 |
|
| B4: | 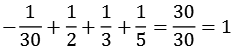 |
|
| B6: | 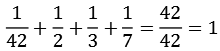 |
|
| B10: | 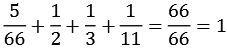 |
|
| B12: | 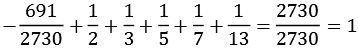 |
|
| B14: | 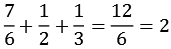 |
|
| B16: | 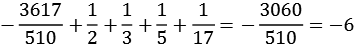 |
|
| B18: |  |
|
| B20: | 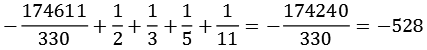 |
|
| B22: | 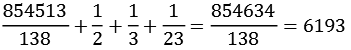 |
Eine andere Definition der Bernoulli-Zahlen (Bernoulli-ex.py).
![]()
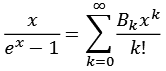
Die Bernoulli-Zahlen lassen sich auch rekursiv berechnen (mit B0 = 1).
![]()
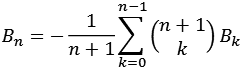
Ein paar Beispiele
![]()
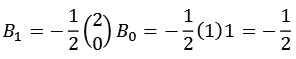
![]()

![]()
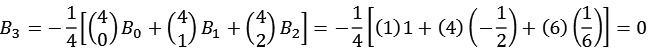
![]()
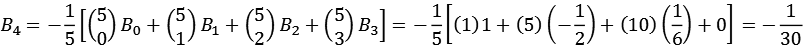
| [zurück] | [Inhaltsverzeichnis] | [vor] |