| [zurück] | 9. Die Primzahlen |
[vor] |
Die Primzahlen [] sind natürliche Zahlen die nur durch 1 und durch sich selbst teilbar sind. Die ersten 10000 Primzahlen (Primzahlen.py).
![]() 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79,
83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223,
227, 229, 233, 239, 241, 251, 257, 263, 269, 271
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79,
83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223,
227, 229, 233, 239, 241, 251, 257, 263, 269, 271
Eine Auswertung der ersten 100000 Primzahlen.
| Ziffer | Anzahl (alle) | Anzahl (letzte) |
| 0 1 2 3 4 5 6 7 8 9 |
46188 102370 55213 72717 47647 47525 47269 72319 47174 72062 |
0 24967 1 25007 0 1 0 25015 0 25009 |
Primfaktorzerlegung [53]: Jede positive natürliche Zahl läßt sich als Produkt aus Primzahlen darstellen (Primfaktorzerlegung.py).
Ein paar Beispiele.
| 30 | 2 * 3 * 5 |
| 1001 | 7 * 11 * 13 |
| 6936 | 2 * 2 * 2 * 3 * 17 * 17 |
| 10000 | 2 * 2 * 2 * 2 * 5 * 5 * 5 * 5 |
| 11227 | 103 * 109 |
Goldbachsche Vermutung
Es gibt eine starke und schwache Goldbachsche Vermutung, die starke lautet:
![]() Jede gerade Zahl, die größer als 2 ist, ist die Summe zweier Primzahlen, z.B.
Jede gerade Zahl, die größer als 2 ist, ist die Summe zweier Primzahlen, z.B.
| 4 = 2 + 2 | 24 = 5 + 19 24 = 7 + 17 24 = 11 + 13 |
| 6 = 3 + 3 | 26 = 3 + 23 26 = 7 + 19 26 = 13 + 13 |
| 8 = 3 + 5 | 28 = 5 + 23 28 = 11 + 17 |
| 10 = 5 + 5 | 30 = 7 + 23 30 = 11 + 19 30 = 13 + 17 |
| 12 = 5 + 7 | 32 = 3 + 29 32 = 13 + 19 |
| 14 = 3 + 11 14 = 7 + 7 |
34 = 3 + 31 34 = 5 + 29 34 = 11 + 23 34 = 17 + 17 |
| 16 = 3 + 13 16 = 5 + 11 |
36 = 5 + 31 36 = 7 + 29 36 = 13 + 23 36 = 17 + 19 |
| 18 = 5 + 13 18 = 7 + 11 |
38 = 7 + 31 38 = 19 + 19 |
| 20 = 3 + 17 20 = 7 + 13 |
40 = 3 + 37 40 = 11 + 29 40 = 17 + 23 |
| 22 = 3 + 19 22 = 5 + 17 22 = 11 + 11 |
42 = 5 + 37 42 = 11 + 31 42 = 13 + 29 42 = 19 + 23 |
Die schwache Goldbachsche Vermutung lautet:
![]() Jede ungerade Zahl, die größer als 5 ist, ist die Summe dreier Primzahlen, z.B.
Jede ungerade Zahl, die größer als 5 ist, ist die Summe dreier Primzahlen, z.B.
| 7 = 2 + 2 + 3 | 27 = 2 + 2 + 23 27 = 3 + 3 + 19 27 = 3 + 5 + 17 27 = 7 + 7 + 13 |
| 9 = 2 + 2 + 5 9 = 3 + 3 + 3 |
29 = 5 + 5 + 19 29 = 5 + 7 + 17 29 = 5 + 11 + 13 29 = 7 + 11 + 11 |
| 11 = 3 + 3 + 5 | 31 = 3 + 5 + 23 31 = 5 + 7 + 19 31 = 7 + 7 + 17 31 = 7 + 11 + 13 |
| 13 = 3 + 3 + 7 13 = 3 + 5 + 5 |
33 = 2 + 2 + 29 33 = 5 + 5 + 23 33 = 7 + 7 + 19 33 = 5 + 11 + 17 33 = 7 + 13 + 13 33 = 11 + 11 + 11 |
| 15 = 2 + 2 + 11 15 = 3 + 5 + 7 15 = 5 + 5 + 5 |
35 = 2 + 2 + 31 35 = 3 + 3 + 29 35 = 5 + 7 + 23 35 = 5 + 11 + 19 35 = 7 + 11 + 17 35 = 11 + 11 + 13 |
| 17 = 2 + 2 + 13 17 = 3 + 7 + 7 17 = 3 + 3 + 11 |
37 = 3 + 3 + 31 37 = 3 + 5 + 29 37 = 7 + 7 + 23 37 = 7 + 11 + 19 37 = 7 + 13 + 17 37 = 11 + 13 + 13 |
| 19 = 3 + 3 + 13 19 = 3 + 5 + 11 19 = 5 + 7 + 7 |
39 = 3 + 5 + 31 39 = 5 + 5 + 29 39 = 5 + 11 + 23 39 = 7 + 13 + 19 39 = 11 + 11 + 17 39 = 13 + 13 + 13 |
| 21 = 2 + 2 + 17 21 = 7 + 7 + 7 |
41 = 2 + 2 + 37 41 = 5 + 5 + 31 41 = 5 + 7 + 29 41 = 5 + 13 + 23 41 = 5 + 17 + 19 41 = 7 + 11 + 23 41 = 11 + 11 + 19 41 = 11 + 13 + 17 |
| 23 = 5 + 5 + 13 23 = 3 + 3 + 17 23 = 5 + 7 + 11 |
43 = 3 + 3 + 37 43 = 3 + 11 + 29 43 = 3 + 17 + 23 43 = 5 + 7 + 31 43 = 7 + 7 + 29 43 = 7 + 13 + 23 43 = 7 + 17 + 19 43 = 11 + 13 + 19 43 = 13 + 13 + 17 |
| 25 = 7 + 7 + 11 25 = 3 + 5 + 17 25 = 5 + 7 + 13 |
45 = 2 + 2 + 41 45 = 3 + 5 + 37 45 = 3 + 11 + 31 45 = 3 + 19 + 23 45 = 5 + 11 + 29 45 = 5 + 17 + 23 45 = 7 + 7 + 31 45 = 11 + 11 + 23 45 = 13 + 13 + 19 |
Von Goldbachsch gibt es noch eine weitere Vermutung die aber inzwischen widerlegt wurde:
![]() Jede ungerade Zahl n läßt sich als Summe aus einer Primzahl p und dem Doppelten einer Quadratzahl darstellen. n = p + 2*b2
Jede ungerade Zahl n läßt sich als Summe aus einer Primzahl p und dem Doppelten einer Quadratzahl darstellen. n = p + 2*b2
Wenn man b = 0 zuläßt gibt für diese Vermutung mit 5777 und 5993 nur zwei Ausnahmen. Alle Primzahlen erfüllen diese Vermutung da p = p + 2*02.
Wenn b ungleich 0 gilt kommem weitere 8 Zahlen (2, 3, 17, 137, 227, 977, 1187, 1493) hinzu, diese Zahlen nennt man Stern Primzahlen da es alles Primzahlen sind. Nimmt man 5777 und 5993, die keine Primzahlen sind, hinzu erhält man die Stern Zahlen.
John Friedlander und Henryk Iwaniec Vermutung
![]() Es gibt unendlich viele Primzahlen der Form a2 + b4, wobei a und b natürliche Zahlen sind.
Es gibt unendlich viele Primzahlen der Form a2 + b4, wobei a und b natürliche Zahlen sind.
Diese Vermutung wurde bewiesen. Ein paar Beispiele:
|
2 = 12 + 14 5 = 22 + 14 17 = 42 + 14 17 = 12 + 24 37 = 62 + 14 41 = 52 + 24 97 = 92 + 24 97 = 42 + 34 101 = 102 + 14 137 = 112 + 24 181 = 102 + 34 197 = 142 + 14 241 = 152 + 24 257 = 162 + 14 257 = 12 + 44 277 = 142 + 34 281 = 52 + 44 337 = 162 + 34 337 = 92 + 44 401 = 202 + 14 |
457 = 212 + 24 577 = 242 + 14 617 = 192 + 44 641 = 252 + 24 641 = 42 + 54 661 = 62 + 54 677 = 262 + 14 757 = 262 + 34 769 = 122 + 54 821 = 132 + 54 857 = 292 + 24 881 = 252 + 44 881 = 162 + 54 977 = 312 + 24 1097 = 292 + 44 1109 = 222 + 54 1201 = 242 + 54 1217 = 312 + 44 1237 = 342 + 34 1297 = 362 + 14 |
1297 = 12 + 64 1301 = 262 + 54 1321 = 52 + 64 1409 = 282 + 54 1481 = 352 + 44 1601 = 402 + 14 1657 = 192 + 64 1697 = 412 + 24 1777 = 392 + 44 2017 = 442 + 34 2069 = 382 + 54 2137 = 292 + 64 2281 = 452 + 44 2389 = 422 + 54 2417 = 492 + 24 2417 = 42 + 74 2437 = 62 + 74 |
![]() Es gibt unendlich viele Primzahlen der Form a2 + 4b2, wenn a und b Primzahlen sind.
Es gibt unendlich viele Primzahlen der Form a2 + 4b2, wenn a und b Primzahlen sind.
Diese Vermutung wurde bisher nicht bewiesen. Ein paar Beispiele:
|
41 = 52 + 4*22 61 = 52 + 4*32 109 = 32 + 4*52 137 = 112 + 4*22 149 = 72 + 4*52 157 = 112 + 4*32 221 = 112 + 4*52 269 = 132 + 4*52 317 = 112 + 4*72 389 = 172 + 4*52 397 = 192 + 4*32 461 = 192 + 4*52 509 = 52 + 4*112 557 = 192 + 4*72 653 = 132 + 4*112 701 = 52 + 4*132 773 = 172 + 4*112 797 = 112 + 4*132 857 = 292 + 4*22 877 = 292 + 4*32 941 = 292 + 4*52 977 = 312 + 4*22 997 = 312 + 4*32 1013 = 232 + 4*112 1061 = 312 + 4*52 1181 = 52 + 4*172 |
1277 = 112 + 4*172 1453 = 32 + 4*192 1493 = 72 + 4*192 1613 = 132 + 4*192 1637 = 312 + 4*132 1697 = 412 + 4*22 1733 = 172 + 4*192 1877 = 412 + 4*72 1949 = 432 + 4*52 1973 = 232 + 4*192 1997 = 292 + 4*172 2141 = 52 + 4*232 2237 = 112 + 4*232 2309 = 472 + 4*52 2333 = 432 + 4*112 2357 = 412 + 4*132 2477 = 192 + 4*232 2693 = 472 + 4*112 2837 = 412 + 4*172 2909 = 532 + 4*52 2957 = 292 + 4*232 3373 = 32 + 4*292 3389 = 52 + 4*292 3413 = 72 + 4*292 3517 = 592 + 4*32 3533 = 132 + 4*292 |
3581 = 592 + 4*52 3677 = 592 + 4*72 3797 = 412 + 4*232 3821 = 612 + 4*52 3853 = 32 + 4*312 3893 = 72 + 4*312 3917 = 612 + 4*72 4013 = 132 + 4*312 4133 = 172 + 4*312 4157 = 592 + 4*132 4253 = 532 + 4*192 4373 = 232 + 4*312 4397 = 612 + 4*132 4637 = 592 + 4*172 4733 = 372 + 4*292 4877 = 612 + 4*172 4973 = 672 + 4*112 5077 = 712 + 4*32 5237 = 712 + 4*72 5501 = 52 + 4*372 5573 = 472 + 4*292 5693 = 432 + 4*312 5717 = 712 + 4*132 5813 = 732 + 4*112 6053 = 472 + 4*312 6173 = 532 + 4*292 |
6197 = 712 + 4*172 6257 = 792 + 4*22 6277 = 792 + 4*32 6317 = 292 + 4*372 6653 = 532 + 4*312 6733 = 32 + 4*412 6917 = 792 + 4*132 7013 = 172 + 4*412 7253 = 232 + 4*412 7517 = 112 + 4*432 7757 = 192 + 4*432 7853 = 672 + 4*292 7937 = 892 + 4*22 8093 = 372 + 4*412 8117 = 892 + 4*72 8237 = 292 + 4*432 8353 = 312 + 4*432 8573 = 432 + 4*412 8597 = 892 + 4*132 8693 = 732 + 4*292 8861 = 52 + 4*472 8933 = 472 + 4*412 9173 = 732 + 4*312 9533 = 532 + 4*412 9677 = 292 + 4*472 |
Trunkierbare Primzahlen
Eine trunkierbare Primzahl ist eine Primzahl, die nach Abschneiden von Ziffern eine Primzahl bleibt. Dabei unterscheidet man rechtstrunkierbare, linkstrunkierbare und beidseitig trunkierbare Primzahlen.
Es gibt genau 83 rechtstrunkierbare Primzahlen.
| 2 71 379 2399 7331 37337 293999 2339933 37337999 |
3 73 593 2939 7333 37339 373379 2399333 59393339 |
5 79 599 3119 7393 37397 373393 2939999 73939133 |
7 233 719 3137 23333 59393 593933 3733799 |
23 239 733 3733 23339 59399 593993 5939333 |
29 293 739 3739 23399 71933 719333 7393913 |
31 311 797 3793 23993 73331 739391 7393931 |
37 313 2333 3797 29399 73939 739393 7393933 |
53 17 2339 5939 31193 233993 739397 23399339 |
59 373 2393 7193 31379 239933 739399 29399999 |
Ich habe bei den rechtstrunkierbaren Primzahlen ausgewertet welche Ziffern wie häufig in den Zahlen vorkommen.
| Ziffer | Anzahl (alle) | Anzahl (letzte) |
| 0 1 2 3 4 5 6 7 8 9 |
0 22 24 156 0 12 0 49 0 107 |
0 7 1 35 0 1 0 9 0 30 |
Ausser der 2, die selbst eine Primzahl ist, kommen keine weiteren geraden Zahlen vor. Die 2 steht auch immer am Anfang der Primzahl. Die 3 und die 9 kommen am häufigsten vor.
Bei den linkstrunkierbaren Primzahlen (es gibt 4260) sieht das etwas anders aus, die Null ist dabei per Definition ausgeschlossen.
| Ziffer | Anzahl (alle) | Anzahl (letzte) |
| 0 1 2 3 4 5 6 7 8 9 |
0 3554 2999 7748 3259 2917 6752 5509 3040 5361 |
0 0 1 2127 0 1 0 2131 0 0 |
Die 2 und die 5 kommen nur einmal vor, damit sind die einstelligen Primzahlen 2 und 5 gemeint. Die 9 kommt als letztes Ziffer nicht vor da sie selbst keine Primzahl ist.
Die 5 kann nicht letzte Ziffer sein da alle zweistelligen Zahlen mit einer 5 am Ende keine Primzahlen sind. Sie sind durch 5 teilbar.
Sophie Germain Primzahlen
Eine Primzahl p nennt man Sophie-Germain-Primzahl, wenn auch 2p + 1 eine Primzahl ist (2p + 1 ist dann eine sichere Primzahl).
Eine Auswertung der ersten 100000 Sophie Germain Primzahlen.
| Ziffer | Anzahl (alle) | Anzahl (letzte) |
| 0 1 2 3 4 5 6 7 8 9 |
54079 138767 60752 93763 59858 59940 59509 59541 59060 89542 |
0 33343 1 33407 0 1 0 0 0 33248 |
Als letzte Ziffern kommen nur die Zahlen 1, 3 und 9 in Frage. Alle drei Zahlen (1, 3, 9) kommen fast gleich häufig vor.
Die 2 und die 5 kommen nur einmal, als Primzahl 2 und 5, vor.
Zahlen mit geraden Zahlen (0, 2, 4, 6, 8) am Ende können keine Primzahlen sein (bis auf die Primzahl 2).
Bleibt noch die Frage warum es keine Sophie Germain Primzahlen mit einer 7 am Ende gibt. Ein paar Beispiele.
| p | q = 2p + 1 | Primfaktoren |
| 17 37 47 67 97 107 127 137 157 167 |
35 75 95 135 195 215 255 275 315 335 |
5, 7 3, 5, 5 5, 19 3, 3, 3, 5 3, 5, 13 5, 43 3, 5, 17 5, 5, 11 3, 3, 5, 7 5, 67 |
Dieser Zusammenhang läßt sich leicht beweisen.
p = 10k + 7
q = 2p + 1 = 20k + 14 + 1
q = 20k + 15 = 5(4k + 3)
D.h. q ist immer durch 5 teilbar und kann daher keine Primzahl sein.
Repunit Primzahlen
Repunit Zahlen sind Zahlen die nur die Ziffer 1 enthalten, sie sind wie folgt definiert.
![]()
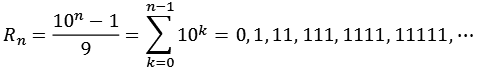
Die Repunit Zahlen lassen sich auch rekursiv berechnen.
![]()
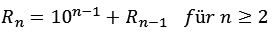
![]()
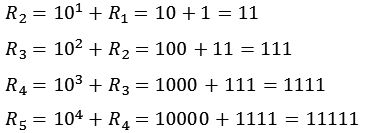
Ein sehr kleiner Teil der Repunit Zahlen sind Primzahlen, z.B. Rn mit n = 2, 19, 23, 317, 1031, ...
Die Repunit Zahlen von R1 bis R25 mit ihrer Primfaktorzerlegung, die 3 Primzahlen sind blau dargestellt.
| n | Rn | Primfaktorzerlegung |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
1 11 111 1111 11111 111111 1111111 11111111 111111111 1111111111 11111111111 111111111111 1111111111111 11111111111111 111111111111111 1111111111111111 11111111111111111 111111111111111111 1111111111111111111 11111111111111111111 111111111111111111111 1111111111111111111111 11111111111111111111111 111111111111111111111111 1111111111111111111111111 |
1 11 3, 37 11, 101 41, 271 3, 7, 11, 13, 37 239, 4649 11, 73, 101, 137 3, 3, 37, 333667 11, 41, 271, 9091 21649, 513239 3, 7, 11, 13, 37, 101, 9901 53, 79, 265371653 11, 239, 4649, 909091 3, 31, 37, 41, 271, 2906161 11, 17, 73, 101, 137, 5882353 2071723, 5363222357 3, 3, 7, 11, 13, 19, 37, 52579, 333667 1111111111111111111 11, 41, 101, 271, 3541, 9091, 27961 3, 37, 43, 239, 1933, 4649, 10838689 11, 11, 23, 4093, 8779, 21649, 513239 11111111111111111111111 3, 7, 11, 13, 37, 73, 101, 137, 9901, 99990001 41, 271, 21401, 25601, 182521213001 |
Pythagoreische Primzahlen
Eine pythagoreische Primzahl ist wie folgt definiert: p = 4 n + 1.
Jede pythagoreische Primzahl kann als Summe von zwei Quadraten dargestellt werden (p = a2 + b2).
Die Primzahlen sind blau dargestellt.
| n | 4 n + 1 | a2 + b2 |
| 1 | 4*1 + 1 = 5 | 12 + 22 = 5 |
| 2 | 4*2 + 1 = 9 | |
| 3 | 4*3 + 1 = 13 | 22 + 32 = 13 |
| 4 | 4*4 + 1 = 17 | 12 + 42 = 17 |
| 5 | 4*5 + 1 = 21 | |
| 6 | 4*6 + 1 = 25 | |
| 7 | 4*7 + 1 = 29 | 22 + 52 = 29 |
| 8 | 4*8 + 1 = 33 | |
| 9 | 4*9 + 1 = 37 | 12 + 62 = 37 |
| 10 | 4*10 + 1 = 41 | 42 + 52 = 41 |
| 11 | 4*11 + 1 = 45 | |
| 12 | 4*12 + 1 = 47 | |
| 13 | 4*13 + 1 = 53 | 42 + 72 = 53 |
| 14 | 4*14 + 1 = 57 | |
| 15 | 4*15 + 1 = 61 | 52 + 62 = 61 |
| 16 | 4*16 + 1 = 65 | |
| 17 | 4*17 + 1 = 69 | |
| 18 | 4*18 + 1 = 73 | 32 + 82 = 73 |
| 19 | 4*19 + 1 = 77 | |
| 20 | 4*20 + 1 = 81 | |
| 21 | 4*21 + 1 = 85 | |
| 22 | 4*22 + 1 = 89 | 52 + 82 = 89 |
| 23 | 4*23 + 1 = 93 | |
| 24 | 4*24 + 1 = 97 | 42 + 92 = 97 |
| 25 | 4*25 + 1 = 101 | 12 + 102 = 101 |
| 26 | 4*26 + 1 = 105 | |
| 27 | 4*27 + 1 = 109 | 32 + 102 = 109 |
| 28 | 4*28 + 1 = 113 | 72 + 82 = 113 |
| 29 | 4*29 + 1 = 117 | |
| 30 | 4*30 + 1 = 121 | |
| 31 | 4*31 + 1 = 125 | |
| 32 | 4*32 + 1 = 129 | |
| 33 | 4*33 + 1 = 133 | |
| 34 | 4*34 + 1 = 137 | 42 + 112 = 137 |
| 35 | 4*35 + 1 = 141 | |
| 36 | 4*36 + 1 = 145 | |
| 37 | 4*37 + 1 = 149 | 72 + 102 = 149 |
| 38 | 4*38 + 1 = 153 | |
| 39 | 4*39 + 1 = 157 | 62 + 112 = 157 |
| 40 | 4*40 + 1 = 161 | |
| 41 | 4*41 + 1 = 165 | |
| 42 | 4*42 + 1 = 169 | |
| 43 | 4*43 + 1 = 173 | 22 + 132 = 173 |
| 44 | 4*44 + 1 = 177 | |
| 45 | 4*45 + 1 = 181 | 92 + 102 = 181 |
| 46 | 4*46 + 1 = 185 | |
| 47 | 4*47 + 1 = 189 | |
| 48 | 4*48 + 1 = 193 | 72 + 122 = 193 |
| 49 | 4*49 + 1 = 197 | 12 + 142 = 197 |
| 50 | 4*50 + 1 = 201 |
Bis n = 50 gibt es 21 Primzahlen.
Nicht pythagoreische Primzahlen
Eine nicht pythagoreische Primzahl ist wie folgt definiert: p = 4 n + 3.
Die Primzahlen sind blau dargestellt.
| n | 4 n + 3 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
4*1 + 3 = 7 4*2 + 3 = 11 4*3 + 3 = 15 4*4 + 3 = 19 4*5 + 3 = 23 4*6 + 3 = 27 4*7 + 3 = 31 4*8 + 3 = 35 4*9 + 3 = 39 4*10 + 3 = 43 4*11 + 3 = 47 4*12 + 3 = 51 4*13 + 3 = 55 4*14 + 3 = 59 4*15 + 3 = 63 4*16 + 3 = 67 4*17 + 3 = 71 4*18 + 3 = 75 4*19 + 3 = 79 4*20 + 3 = 83 4*21 + 3 = 87 4*22 + 3 = 91 4*23 + 3 = 95 4*24 + 3 = 99 4*25 + 3 = 103 4*26 + 3 = 107 4*27 + 3 = 111 4*28 + 3 = 115 4*29 + 3 = 119 4*30 + 3 = 123 4*31 + 3 = 127 4*32 + 3 = 131 4*33 + 3 = 135 4*34 + 3 = 139 4*35 + 3 = 143 4*36 + 3 = 147 4*37 + 3 = 151 4*38 + 3 = 155 4*39 + 3 = 159 4*40 + 3 = 163 4*41 + 3 = 167 4*42 + 3 = 171 4*43 + 3 = 175 4*44 + 3 = 179 4*45 + 3 = 183 4*46 + 3 = 187 4*47 + 3 = 191 4*48 + 3 = 195 4*49 + 3 = 199 4*50 + 3 = 203 |
Bis n = 50 gibt es 23 Primzahlen.
Fermat Primzahlen
Eine Fermat Zahl ist wie folgt definiert:
![]()
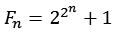
n ist eine natürliche Zahl. Nur die ersten 5 Fermat Zahlen sind Primzahlen.
| n | Fn |
|
0 1 2 3 4 5 6 7 8 |
3 5 17 257 65537 4294967297 18446744073709551617 340282366920938463463374607431768211457 115792089237316195423570985008687907853269984665640564039457584007913129639937 |
Fermat glaubte ursprünglich das alle Fermat Zahlen Primzahlen sind, das hat dann aber Leonhard Euler für F5 widerlegt.
![]() F5 = 4294967297 = 641 * 6700417
F5 = 4294967297 = 641 * 6700417
![]() F6 = 18446744073709551617 = 274177 * 67280421310721
F6 = 18446744073709551617 = 274177 * 67280421310721
Der Kehrwert der Primzahlen
Die Kehrwerte der Primzahlen haben unterschiedliche Periodenlängen.
| Primzahl | Periodenlänge | Kehrwert |
|
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 |
0 1 0 6 2 6 16 18 22 28 15 3 5 21 46 13 58 60 33 35 8 13 41 44 96 4 |
0,5 0,33333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333 0,2 0,14285714285714285714285714285714285714285714285714285714285714285714285714285714285714285714285714286 0,09090909090909090909090909090909090909090909090909090909090909090909090909090909090909090909090909091 0,07692307692307692307692307692307692307692307692307692307692307692307692307692307692307692307692307692 0,05882352941176470588235294117647058823529411764705882352941176470588235294117647058823529411764705882 0,05263157894736842105263157894736842105263157894736842105263157894736842105263157894736842105263157895 0,04347826086956521739130434782608695652173913043478260869565217391304347826086956521739130434782608696 0,03448275862068965517241379310344827586206896551724137931034482758620689655172413793103448275862068966 0,03225806451612903225806451612903225806451612903225806451612903225806451612903225806451612903225806452 0,02702702702702702702702702702702702702702702702702702702702702702702702702702702702702702702702702703 0,02439024390243902439024390243902439024390243902439024390243902439024390243902439024390243902439024390 0,02325581395348837209302325581395348837209302325581395348837209302325581395348837209302325581395348837 0,02127659574468085106382978723404255319148936170212765957446808510638297872340425531914893617021276596 0,01886792452830188679245283018867924528301886792452830188679245283018867924528301886792452830188679245 0,01694915254237288135593220338983050847457627118644067796610169491525423728813559322033898305084745763 0,01639344262295081967213114754098360655737704918032786885245901639344262295081967213114754098360655738 0,01492537313432835820895522388059701492537313432835820895522388059701492537313432835820895522388059701 0,01408450704225352112676056338028169014084507042253521126760563380281690140845070422535211267605633803 0,01369863013698630136986301369863013698630136986301369863013698630136986301369863013698630136986301370 0,01265822784810126582278481012658227848101265822784810126582278481012658227848101265822784810126582278 0,01204819277108433734939759036144578313253012048192771084337349397590361445783132530120481927710843373 0,01123595505617977528089887640449438202247191011235955056179775280898876404494382022471910112359550562 0,01030927835051546391752577319587628865979381443298969072164948453608247422680412371134020618556701031 0,00990099009900990099009900990099009900990099009900990099009900990099009900990099009900990099009900990 |
Die Periodenlänge 1, 2, 3 und 4 treten insgesamt nur einmal auf.
Quartische Primzahlen
Quartische Primzahlen sind wie folgt definiert.
![]() p = x4 + y4 mit ganzzahligen x und y.
p = x4 + y4 mit ganzzahligen x und y.
Ein paar Beispiele.
Primzahlzwillinge
Ein Primzahlzwilling sind zwei Primzahlen, deren Differenz 2 ist. Die ersten Primzahlzwillinge (p, p + 2):
![]() (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193),
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193),
![]() (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571),
(197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571),
![]() (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883), (1019, 1021), (1031, 1033),
(599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883), (1019, 1021), (1031, 1033),
![]() (1049, 1051), (1061, 1063), (1091, 1093), (1151, 1153), (1229, 1231), (1277, 1279), (1289, 1291), (1301, 1303), (1319, 1321), (1427, 1429),
(1049, 1051), (1061, 1063), (1091, 1093), (1151, 1153), (1229, 1231), (1277, 1279), (1289, 1291), (1301, 1303), (1319, 1321), (1427, 1429),
![]() (1451, 1453), (1481, 1483), (1487, 1489), (1607, 1609), (1619, 1621), (1667, 1669), (1697, 1699), (1721, 1723), (1787, 1789), (1871, 1873),
(1451, 1453), (1481, 1483), (1487, 1489), (1607, 1609), (1619, 1621), (1667, 1669), (1697, 1699), (1721, 1723), (1787, 1789), (1871, 1873),
![]() (1877, 1879), (1931, 1933), (1949, 1951), (1997, 1999), (2027, 2029), (2081, 2083), (2087, 2089), (2111, 2113), (2129, 2131), (2141, 2143),
(1877, 1879), (1931, 1933), (1949, 1951), (1997, 1999), (2027, 2029), (2081, 2083), (2087, 2089), (2111, 2113), (2129, 2131), (2141, 2143),
![]() (2237, 2239), (2267, 2269), (2309, 2311), (2339, 2341), (2381, 2383), (2549, 2551), (2591, 2593), (2657, 2659), (2687, 2689), (2711, 2713),
(2237, 2239), (2267, 2269), (2309, 2311), (2339, 2341), (2381, 2383), (2549, 2551), (2591, 2593), (2657, 2659), (2687, 2689), (2711, 2713),
![]() (2729, 2731), (2789, 2791), (2801, 2803), (2969, 2971), (2999, 3001), (3119, 3121), (3167, 3169), (3251, 3253), (3257, 3259), (3299, 3301),
(2729, 2731), (2789, 2791), (2801, 2803), (2969, 2971), (2999, 3001), (3119, 3121), (3167, 3169), (3251, 3253), (3257, 3259), (3299, 3301),
![]() (3329, 3331), (3359, 3361), (3371, 3373), (3389, 3391), (3461, 3463), (3467, 3469), (3527, 3529), (3539, 3541), (3557, 3559), (3581, 3583),
(3329, 3331), (3359, 3361), (3371, 3373), (3389, 3391), (3461, 3463), (3467, 3469), (3527, 3529), (3539, 3541), (3557, 3559), (3581, 3583),
![]() (3671, 3673), (3767, 3769), (3821, 3823), (3851, 3853), (3917, 3919), (3929, 3931), (4001, 4003), (4019, 4021), (4049, 4051), (4091, 4093),
(3671, 3673), (3767, 3769), (3821, 3823), (3851, 3853), (3917, 3919), (3929, 3931), (4001, 4003), (4019, 4021), (4049, 4051), (4091, 4093),
![]() (4127, 4129), (4157, 4159), (4217, 4219), (4229, 4231), (4241, 4243), (4259, 4261), (4271, 4273), (4337, 4339), (4421, 4423), (4481, 4483),
(4127, 4129), (4157, 4159), (4217, 4219), (4229, 4231), (4241, 4243), (4259, 4261), (4271, 4273), (4337, 4339), (4421, 4423), (4481, 4483),
![]() (4517, 4519), (4547, 4549), (4637, 4639), (4649, 4651), (4721, 4723), (4787, 4789), (4799, 4801), (4931, 4933), (4967, 4969)
(4517, 4519), (4547, 4549), (4637, 4639), (4649, 4651), (4721, 4723), (4787, 4789), (4799, 4801), (4931, 4933), (4967, 4969)
Nur die Primzahl 5 taucht zweimal auf. Alle Primzahlzwillinge größer (3, 5) lassen sich wie folgt darstellen: (6n - 1, 6n + 1)
| n | 6 n - 1 | 6 n + 1 |
|
1 2 3 5 7 10 12 17 18 23 25 30 32 33 38 40 45 47 52 58 70 72 77 87 95 100 103 107 110 135 137 138 143 147 170 172 175 177 182 192 205 213 215 217 220 238 242 247 248 268 |
5 11 17 29 41 59 71 101 107 137 149 179 191 197 227 239 269 281 311 347 419 431 461 521 569 599 617 641 659 809 821 827 857 881 1019 1031 1049 1061 1091 1151 1229 1277 1289 1301 1319 1427 1451 1481 1487 1607 |
7 13 19 31 43 61 73 103 109 139 151 181 193 199 229 241 271 283 313 349 421 433 463 523 571 601 619 643 661 811 823 829 859 883 1021 1033 1051 1063 1093 1153 1231 1279 1291 1303 1321 1429 1453 1483 1489 1609 |
Primzahlencousin
Primzahlencousins sind zwei Primzahlen, deren Differenz 4 ist. Die ersten Primzahlencousins (p, p + 4):
![]() (3, 7), (7, 11), (13, 17), (19, 23), (37, 41), (43, 47), (67, 71), (79, 83), (97, 101), (103, 107), (109, 113), (127, 131), (163, 167),
(3, 7), (7, 11), (13, 17), (19, 23), (37, 41), (43, 47), (67, 71), (79, 83), (97, 101), (103, 107), (109, 113), (127, 131), (163, 167),
![]() (193, 197), (223, 227), (229, 233), (277, 281), (307, 311), (313, 317), (349, 353), (379, 383), (397, 401), (439, 443), (457, 461),
(193, 197), (223, 227), (229, 233), (277, 281), (307, 311), (313, 317), (349, 353), (379, 383), (397, 401), (439, 443), (457, 461),
![]() (463, 467), (487, 491), (499, 503), (613, 617), (643, 647), (673, 677), (739, 743), (757, 761), (769, 773), (823, 827), (853, 857),
(463, 467), (487, 491), (499, 503), (613, 617), (643, 647), (673, 677), (739, 743), (757, 761), (769, 773), (823, 827), (853, 857),
![]() (859, 863), (877, 881), (883, 887), (907, 911), (937, 941), (967, 971), (1009, 1013), (1087, 1091), (1093, 1097), (1213, 1217), (1279, 1283),
(859, 863), (877, 881), (883, 887), (907, 911), (937, 941), (967, 971), (1009, 1013), (1087, 1091), (1093, 1097), (1213, 1217), (1279, 1283),
![]() (1297, 1301), (1303, 1307), (1423, 1427), (1429, 1433), (1447, 1451), (1483, 1487), (1489, 1493), (1549, 1553), (1567, 1571), (1579, 1583),
(1297, 1301), (1303, 1307), (1423, 1427), (1429, 1433), (1447, 1451), (1483, 1487), (1489, 1493), (1549, 1553), (1567, 1571), (1579, 1583),
![]() (1597, 1601), (1609, 1613), (1663, 1667), (1693, 1697), (1783, 1787), (1867, 1871), (1873, 1877), (1993, 1997), (1999, 2003), (2083, 2087),
(1597, 1601), (1609, 1613), (1663, 1667), (1693, 1697), (1783, 1787), (1867, 1871), (1873, 1877), (1993, 1997), (1999, 2003), (2083, 2087),
![]() (2137, 2141), (2203, 2207), (2239, 2243), (2269, 2273), (2293, 2297), (2347, 2351), (2377, 2381), (2389, 2393), (2437, 2441), (2473, 2477),
(2137, 2141), (2203, 2207), (2239, 2243), (2269, 2273), (2293, 2297), (2347, 2351), (2377, 2381), (2389, 2393), (2437, 2441), (2473, 2477),
![]() (2539, 2543), (2617, 2621), (2659, 2663), (2683, 2687), (2689, 2693), (2707, 2711), (2749, 2753), (2797, 2801), (2833, 2837), (2857, 2861),
(2539, 2543), (2617, 2621), (2659, 2663), (2683, 2687), (2689, 2693), (2707, 2711), (2749, 2753), (2797, 2801), (2833, 2837), (2857, 2861),
![]() (2953, 2957), (3019, 3023), (3037, 3041), (3079, 3083), (3163, 3167), (3187, 3191), (3217, 3221), (3253, 3257), (3319, 3323), (3343, 3347),
(2953, 2957), (3019, 3023), (3037, 3041), (3079, 3083), (3163, 3167), (3187, 3191), (3217, 3221), (3253, 3257), (3319, 3323), (3343, 3347),
![]() (3457, 3461), (3463, 3467), (3529, 3533), (3613, 3617), (3673, 3677), (3697, 3701), (3793, 3797), (3847, 3851), (3877, 3881), (3907, 3911),
(3457, 3461), (3463, 3467), (3529, 3533), (3613, 3617), (3673, 3677), (3697, 3701), (3793, 3797), (3847, 3851), (3877, 3881), (3907, 3911),
![]() (3919, 3923), (3943, 3947)
(3919, 3923), (3943, 3947)
Satz von Green Tao
Es gibt beliebig lange arithmetische Folgen in der Menge der Primzahlen in Form von.
![]() a, a + d, a + 2d, a + 3d,..., a + (k-1)d
a, a + d, a + 2d, a + 3d,..., a + (k-1)d
a ist die initiale Primzahl, d ist der Abstand zur nächsten Primzahl und k die Anzahl der Folgenglieder.
Ein Paar Beispiele.
| a | d | k | Folge |
| 3 3 5 7 7 199 110437 4943 31385539 |
2 4 6 30 150 210 13860 60060 420420 |
3 3 5 6 7 10 12 13 14 |
3, 5, 7 3, 7, 11 5, 11, 17, 23. 29 7, 37, 67, 97, 127, 157 7, 157, 307, 457, 607, 757, 907 199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879, 2089 110437, 124297, 138157, 152017, 165877, 179737, 193597, 207457, 221317, 235177, 249037, 262897 4943, 65003, 125063, 185123, 245183, 305243, 365303, 425363, 485423, 545483, 605543, 665603, 725663 31385539, 31805959, 32226379, 32646799, 33067219, 33487639, 33908059, 34328479, 34748899, 35169319, 35589739, 36010159, 36430579, 36850999 |
Adrian Stoica Vermutung
Für jede ungerade natürliche Zahl n > 1 existieren zwei natürliche Zahlen x und y, so dass gilt
![]() x + y = n
x + y = n
![]() x2 + y2 ist eine Primzahl
x2 + y2 ist eine Primzahl
| n | x | y | x2 + y2 |
| 3 | 1 | 2 | 5 |
| 5 |
1 2 |
4 3 |
17 13 |
| 7 |
1 2 |
6 5 |
37 29 |
| 9 |
2 4 |
7 5 |
53 41 |
| 11 |
1 3 5 |
10 8 6 |
101 73 61 |
| 13 |
3 4 5 |
10 9 8 |
109 97 89 |
| 15 |
1 2 4 7 |
14 13 11 8 |
197 173 137 113 |
| 17 |
1 2 6 7 |
16 15 11 10 |
257 229 157 149 |
| 19 |
2 4 7 9 |
17 15 12 10 |
293 241 193 181 |
Teiler von Primzahlquadraten nach Matt Parker.
Quadriert man eine Primzahl (p > 3), dann ist das Ergebnis immer durch 24 mit Rest 1 teilbar.
| p | p2 | 24 + n + 1 |
|
5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 |
25 49 121 169 289 361 529 841 961 1369 1681 1849 2209 2809 3481 3721 4489 |
24 * 1 + 1 24 * 2 + 1 24 * 5 + 1 24 * 7 + 1 24 * 12 + 1 24 * 15 + 1 24 * 22 + 1 24 * 35 + 1 24 * 40 + 1 24 * 57 + 1 24 * 70 + 1 24 * 77 + 1 24 * 92 + 1 24 * 117 + 1 24 * 145 + 1 24 * 155 + 1 24 * 187 + 1 |
| [zurück] | [Inhaltsverzeichnis] | [vor] |