| [zurück] | 7. Die Riemannsche Zeta-Funktion |
[vor] |
Die Riemannsche Zeta-Funktion [35, 36, 37, 38, 39, 40] ist wie folgt definiert (Zeta.py).
![]()
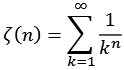
Reihenentwicklung für Zeta(2).
| k = 1 | 1,00000000000 |
| k = 10 | 1,54976773117 |
| k = 100 | 1,63498390018 |
| k = 1000 | 1,64393456668 |
| k = 10000 | 1,64483407185 |
| k = 100000 | 1,64492406690 |
| k = 1000000 | 1,64493306685 |
| k = 10000000 | 1,64493396685 |
| k = 100000000 | 1,64493405783 |
| 1,64493406685 |
Reihenentwicklung für Zeta(3).
| k = 1 | 1,00000000000 |
| k = 10 | 1,19753198567 |
| k = 100 | 1,20200740066 |
| k = 1000 | 1,20205640366 |
| k = 10000 | 1,20205689816 |
| k = 100000 | 1,20205690311 |
| k = 1000000 | 1,20205690315 |
Reihenentwicklung für Zeta(4).
| k = 1 | 1,00000000000 |
| k = 10 | 1,08203658349 |
| k = 100 | 1,08232290534 |
| k = 1000 | 1,08232323338 |
| k = 10000 | 1,08232323371 |
Reihenentwicklung für Zeta(16).
| k = 1 | 1,00000000000 |
| k = 2 | 1,00001525879 |
| k = 3 | 1,00001528202 |
| k = 4 | 1,00001528225 |
| k = 5 | 1,00001528226 |
Für einige Werte der Zeta Funktion gibt es schneller konvergierende Reihen, z.B für Zeta(3). Hier habe ich einfach alle Formeln aufgeführt die ich interessant fand, zu jeder Formel gibt es im Download Bereich ein Python Script.
Zeta1.py
![]()
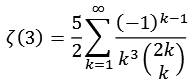
Mit Hilfe der Binominalkoeffizienten läßt sich die Formel umstellen.
![]()
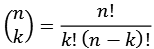
![]()
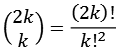
![]()
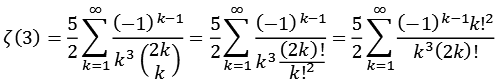
| k = 1 | 1,25000000000 |
| k = 2 | 1,19791666667 |
| k = 3 | 1,20254629630 |
| k = 4 | 1,20198826058 |
| k = 5 | 1,20206762566 |
| k = 6 | 1,20205509961 |
| k = 7 | 1,20205722333 |
| k = 8 | 1,20205684394 |
| k = 9 | 1,20205691447 |
| k = 10 | 1,20205690094 |
| k = 11 | 1,20205690360 |
| k = 12 | 1,20205690307 |
| k = 13 | 1,20205690318 |
| k = 14 | 1,20205690315 |
Zeta2.py
![]()
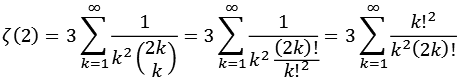
| k = 1 | 1,50000000000 |
| k = 2 | 1,62500000000 |
| k = 3 | 1,64166666667 |
| k = 4 | 1,64434523810 |
| k = 5 | 1,64482142857 |
| k = 6 | 1,64491161616 |
| k = 7 | 1,64492945547 |
| k = 8 | 1,64493309766 |
| k = 9 | 1,64493385942 |
| k = 10 | 1,64493402180 |
| k = 11 | 1,64493405694 |
| k = 12 | 1,64493406465 |
| k = 13 | 1,64493406636 |
| k = 14 | 1,64493406674 |
| k = 15 | 1,64493406682 |
| k = 16 | 1,64493406684 |
| k = 17 | 1,64493406685 |
Zeta3.py
![]()
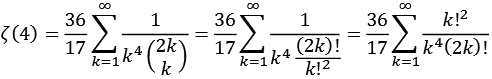
| k = 1 | 1,05882352941 |
| k = 2 | 1,08088235294 |
| k = 3 | 1,08218954248 |
| k = 4 | 1,08230771475 |
| k = 5 | 1,08232116013 |
| k = 6 | 1,08232292851 |
| k = 7 | 1,08232318550 |
| k = 8 | 1,08232322567 |
| k = 9 | 1,08232323231 |
| k = 10 | 1,08232323346 |
| k = 11 | 1,08232323366 |
| k = 12 | 1,08232323370 |
| k = 13 | 1,08232323371 |
Zeta4.py
![]()
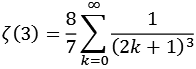
| k = 1 | 1,18518518519 |
| k = 10 | 1,20146779823 |
| k = 100 | 1,20204990122 |
| k = 1000 | 1,20205683187 |
| k = 10000 | 1,20205690245 |
| k = 100000 | 1,20205690315 |
Zeta5.py
![]()
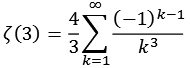
| k = 1 | 1,33333333333 |
| k = 10 | 1,20148863522 |
| k = 100 | 1,20205624649 |
| k = 1000 | 1,20205690249 |
| k = 10000 | 1,20205690315 |
Zeta6.py
![]()
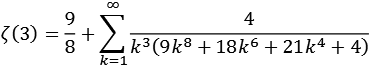
| k = 1 | 1,20192307692 |
| k = 2 | 1,20205479452 |
| k = 3 | 1,20205679988 |
| k = 4 | 1,20205689332 |
| k = 5 | 1,20205690171 |
| k = 6 | 1,20205690287 |
| k = 7 | 1,20205690309 |
| k = 8 | 1,20205690314 |
| k = 9 | 1,20205690315 |
Zeta7.py
![]()
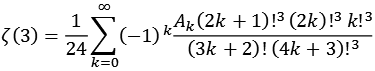
mit
![]()
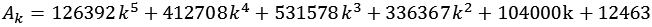
| k = 0 | 1,20206404321 |
| k = 1 | 1,20205690311 |
| k = 2 | 1,20205690315 |
Zeta8.py
![]()
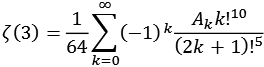
mit
![]()
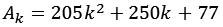
| k = 0 | 1,20312500000 |
| k = 1 | 1,20205600566 |
| k = 2 | 1,20205690394 |
| k = 3 | 1,20205690315 |
Zeta9.py
![]()
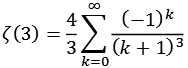
| k = 1 | 1,16666666667 |
| k = 10 | 1,20249038829 |
| k = 100 | 1,20205754061 |
| k = 1000 | 1,20205690382 |
| k = 10000 | 1,20205690315 |
Zeta10.py
![]()
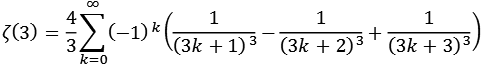
| k = 1 | 1,19970987654 |
| k = 10 | 1,20207461220 |
| k = 100 | 1,20205692701 |
| k = 1000 | 1,20205690318 |
| k = 10000 | 1,20205690315 |
Zeta20.py
![]()

| k = 1 | 1,20148863522 |
| k = 10 | 1,20206080095 |
| k = 100 | 1,20205690832 |
| k = 1000 | 1,20205690316 |
Zeta21.py
![]()
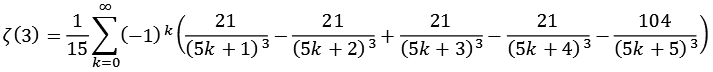
| k = 1 | 1,20322973365 |
| k = 10 | 1,20203932158 |
| k = 100 | 1,20205687671 |
| k = 1000 | 1,20205690313 |
| k = 10000 | 1,20205690316 |
Zeta11.py
![]()
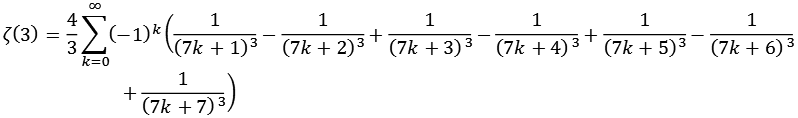
| k = 1 | 1,20183976288 |
| k = 10 | 1,20205833500 |
| k = 100 | 1,20205690504 |
| k = 1000 | 1,20205690315 |
Zeta12.py
![]()
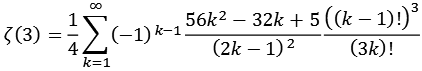
| k = 1 | 1,20833333333 |
| k = 2 | 1,20196759259 |
| k = 3 | 1,20205864198 |
| k = 4 | 1,20205686353 |
| k = 5 | 1,20205690415 |
| k = 6 | 1,20205690313 |
| k = 7 | 1,20205690315 |
Zeta13.py
![]()
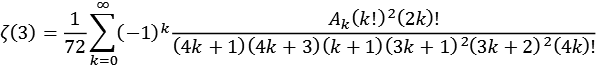
mit
![]()
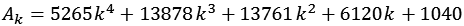
| k = 1 | 1,20204761905 |
| k = 2 | 1,20205697766 |
| k = 3 | 1,20205690245 |
| k = 4 | 1,20205690317 |
| k = 5 | 1,20205690315 |
Zeta14.py
![]()
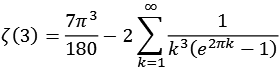
| k = 1 | 1,20205777548 |
| k = 2 | 1,20205690364 |
| k = 3 | 1,20205690315 |
Zeta15.py
![]()
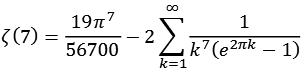
| k = 1 | 1,00834933188 |
| k = 2 | 1,00834927739 |
| k = 3 | 1,00834927738 |
Zeta16.py
![]()
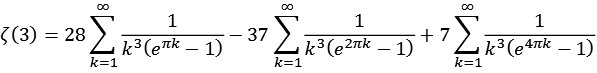
| k = 1 | 1,19543950751 |
| k = 2 | 1,20197165661 |
| k = 3 | 1,20205534282 |
| k = 4 | 1,20205686853 |
| k = 5 | 1,20205690229 |
| k = 6 | 1,20205690314 |
| k = 7 | 1,20205690315 |
Zeta17.py
![]()
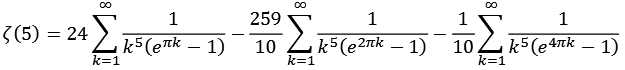
| k = 1 | 1,03551932209 |
| k = 2 | 1,03691970196 |
| k = 3 | 1,03692767223 |
| k = 4 | 1,03692775397 |
| k = 5 | 1,03692775512 |
| k = 6 | 1,03692775514 |
Zeta18.py
![]()
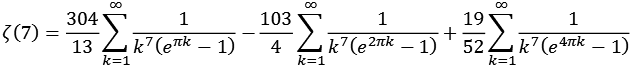
| k = 1 | 1,00800730531 |
| k = 2 | 1,00834840948 |
| k = 3 | 1,00834927236 |
| k = 4 | 1,00834927734 |
| k = 5 | 1,00834927738 |
Zeta19.py
![]()
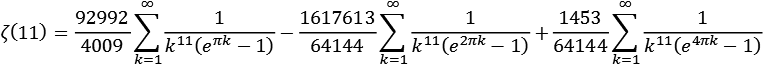
| k = 1 | 1,00047303058 |
| k = 2 | 1,00049417802 |
| k = 3 | 1,00049418858 |
| k = 4 | 1,00049418860 |
Für ganze gerade Zahlen läßt sich die Zeta Funktion mit Hilfe von pi ausdrücken.
![]()
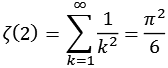
![]()
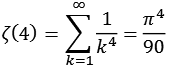
![]()
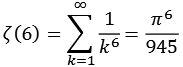
![]()
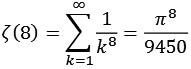
![]()

Bei den Nennern handelt es sich um die Integer Reihe A002432 [41].
Für Zeta(2) gib es eine interessante Berechnung als Doppelreihe.
![]()
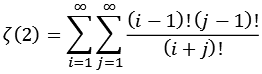
| i, j = 1000 | 1,64293506651 |
Nach 1000 mal 1000 Rechenschritten sind nur 2 Nachkommastellen korrekt.
Es gibt auch einen Zusammenhang zwischen der Riemannschen Zeta-Funktion und den Primzahlen (Zeta-Prim.py).
![]()
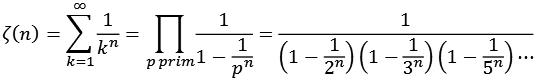
Für die Berechnung habe ich die ersten 10000 Primzahlen verwendet. Nur für n = 2 wird die Geanauigkeit von 11 Stellen nach dem Komma nicht erreicht.
| n = 2 | 1,64493281127 |
| n = 3 | 1,20205690316 |
| n = 4 | 1,08232323371 |
| n = 5 | 1,03692775514 |
| n = 6 | 1,01734306198 |
| n = 7 | 1,00834927738 |
| n = 8 | 1,00407735620 |
| n = 9 | 1,00200839283 |
| n = 10 | 1,00099457513 |
| n = 11 | 1,00049418860 |
| n = 12 | 1,00024608655 |
| n = 13 | 1,00012271335 |
| n = 14 | 1,00006124814 |
| n = 15 | 1,00003058824 |
| n = 16 | 1,00001528226 |
| n = 17 | 1,00000763720 |
| n = 18 | 1,00000381729 |
| n = 19 | 1,00000190821 |
| n = 20 | 1,00000095396 |
Mit Hilfe der Riemannschen Zeta-Funktion läßt sich auch die Kreiszahl pi berechnen (Zeta-Pi.py, Zeta-Prim-Dezimal.py).
![]()
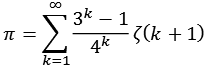
| k = 10 | 2,97263582002642005920410156250 |
| k = 50 | 3,14159095462369478307859026190 |
| k = 100 | 3,14159265358770190323584980612 |
Werte der Zeta Funktion für n = 2 bis n = 17 mit 98 Nachkommastellen.
| n = 2 | 1,64493406684822643647241516664602518921894990120679843773555822937000747040320087383362890061975870 |
| n = 3 | 1,20205690315959428539973816151144999076498629234049888179227155534183820578631309018645587360933526 |
| n = 4 | 1,08232323371113819151600369654116790277475095191872690768297621544412061618696884655690963594169991 |
| n = 5 | 1,03692775514336992633136548645703416805708091950191281197419267790380358978628148456004310655713333 |
| n = 6 | 1,01734306198444913971451792979092052790181749003285356184240866400433218290195789788277397793853517 |
| n = 7 | 1,00834927738192282683979754984979675959986356056523870641728313657160147831735573534609696891385132 |
| n = 8 | 1,00407735619794433937868523850865246525896079064985002032911020265258295257474881439528723037237197 |
| n = 9 | 1,00200839282608221441785276923241206048560585139488875654859661590978505339025839895039306912716958 |
| n = 10 | 1,00099457512781808533714595890031901700601953156447751725778899463629146515191295439704196861038565 |
| n = 11 | 1,00049418860411946455870228252646993646860643575820861711914143610005405979821981470259184302356062 |
| n = 12 | 1,00024608655330804829863799804773967096041608845800340453304095213325201968194091304904280855190069 |
| n = 13 | 1,00012271334757848914675183652635739571427510589550984513670267162089672682984420981289271395326813 |
| n = 14 | 1,00006124813505870482925854510513533374748169616915454948275520225286294102317742087665978297199846 |
| n = 15 | 1,00003058823630702049355172851064506258762794870685817750656993289333226715634227957307233434701754 |
| n = 16 | 1,00001528225940865187173257148763672202323738899047153115310520358878708702795315178628560484632246 |
| n = 17 | 1,00000763719763789976227360029356302921308824909026267909537984397293564329028245934208173863691667 |
Die Zeta Funktion (gerade n) läßt sich auch mit Hilfe der Bernoulli-Zahlen ausdrücken.
![]()
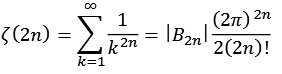
Zum Beispiel.
![]()
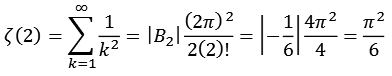
![]()
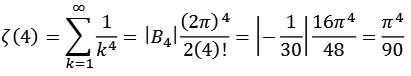
![]()
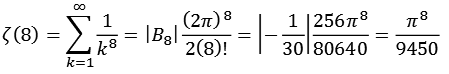
![]()
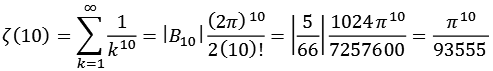
| [zurück] | [Inhaltsverzeichnis] | [vor] |