6. Die Kreiszahl pi
|
[zurück] | 6. Die Kreiszahl pi |
[vor] | |
Die Kreiszahl pi [] lautet.
pi = 3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679
Zur Berechnung von pi gibt es viele interessante Reihenentwicklungen, fangen wir mit den Formeln auf der Basis der arctan Funktion an. Die allgemeine Formel lautet.
Die Nenner bn lassen sich nach der Gleichung b2+1 auf N Primzahlen zurückführen.
Für die Koeffizienten an, bn und cn gilt ausserdem.
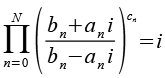
PiAtan1.py
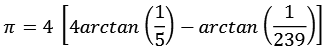
52 + 1 = 26 = 2 * 13
2392 + 1 = 57122 = 2 * 134
In diesem Fall werden die 2 Primzahlen 2 und 13 verwendet.
Für die Koeffizienten an, bn und cn gilt.
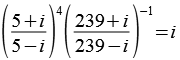
PiAtan2.py
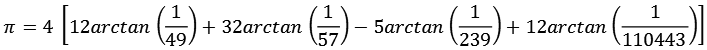
492 + 1 = 2402 = 2 * 1201
572 + 1 = 3250 = 2 * 53 * 13
2392 + 1 = 57122 = 2 · 134
1104432 + 1 = 12197656250 = 2 * 58 * 13 * 1201
In diesem Fall werden die 4 Primzahlen 2, 5, 13 und 1201 verwendet.
Für die Koeffizienten an, bn und cn gilt.
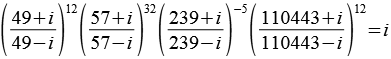
PiAtan3.py
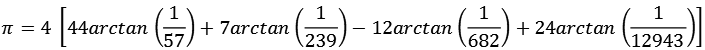
572 + 1 = 3250 = 2 * 53 * 13
2392 + 1 = 57122 = 2 * 134
6822 + 1 = 465125 = 53 * 612
129432 + 1 = 167521250 = 2 * 54 * 133 * 61
In diesem Fall werden die 4 Primzahlen 2, 5, 13 und 61 verwendet.
Für die Koeffizienten an, bn und cn gilt.
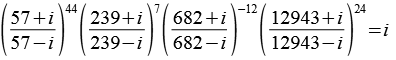
Mit dieser Formel habe ich die Zahl pi auf 1000 Stellen berechnet, dazu waren 300 Iterationen nötig.
PiAtan4.py
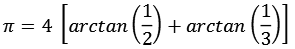
22 + 1 = 5 = 5
32 + 1 = 10 = 2 * 5
In diesem Fall werden die 2 Primzahlen 2 und 5 verwendet.
Für die Koeffizienten an, bn und cn gilt.
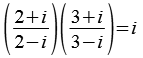
PiAtan5.py
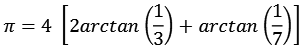
32 + 1 = 10 = 2 * 5
72 + 1 = 50 = 2 * 52
In diesem Fall werden die 2 Primzahlen 2 und 5 verwendet.
Für die Koeffizienten an, bn und cn gilt.
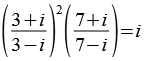
PiAtan6.py
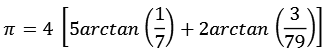
72 + 1 = 50 = 2 * 52
792 + 1 = 6242 = 2 * 3121
In diesem Fall werden die 3 Primzahlen 2, 5 und 3121 verwendet.
Für die Koeffizienten an, bn und cn gilt.
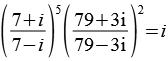
PiAtan7.py
92 + 1 = 82 = 2 * 41
322 + 1 = 1025 = 52 * 41
732 + 1 = 5330 = 2 * 5 * 13 * 41
29432 + 1 = 8661250 = 2 * 54 * 132 * 41
In diesem Fall werden die 4 Primzahlen 2, 5, 13 und 41 verwendet.
Für die Koeffizienten an, bn und cn gilt.
PiAtan8.py
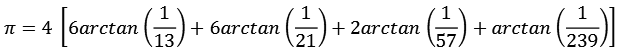
132 + 1 = 170 = 2 * 5 * 17
212 + 1 = 442 = 2 * 13 * 17
572 + 1 = 3250 = 2 * 53 * 13
2392 + 1 = 57122 = 2 * 134
In diesem Fall werden die 4 Primzahlen 2, 5, 13 und 17 verwendet.
Für die Koeffizienten an, bn und cn gilt.
PiAtan9.py
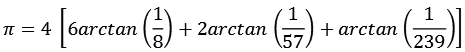
82 + 1 = 65 = 5 * 13
572 + 1 = 3250 = 2 * 53 * 13
2392 + 1 = 57122 = 2 * 134
In diesem Fall werden die 3 Primzahlen 2, 5, und 13 verwendet.
Für die Koeffizienten an, bn und cn gilt.
PiAtan10.py
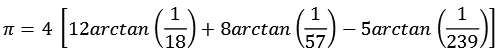
182 + 1 = 325 = 52 * 13
572 + 1 = 3250 = 2 * 53 * 13
2392 + 1 = 57122 = 2 * 134
In diesem Fall werden die 3 Primzahlen 2, 5, und 13 verwendet.
Für die Koeffizienten an, bn und cn gilt.
PiAtan11.py
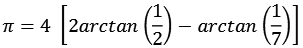
22 + 1 = 5 = 5
72 + 1 = 50 = 2 * 52
In diesem Fall werden die 2 Primzahlen 2 und 5 verwendet.
Für die Koeffizienten an, bn und cn gilt.
PiAtan12.py
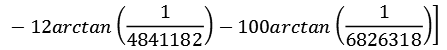
2392 + 1 = 57122 = 2 * 134
10232 + 1 = 1046530 = 2 * 5 * 229 * 457
58322 + 1 = 34012225 = 52 * 13 * 229 * 457
1104432 + 1 = 12197656250 = 2 * 58 * 13 * 1201
48411822 + 1 = 23437043157125 = 53 * 13 * 2293 * 1201
68263182 + 1 = 46598617437125 = 53 * 138 * 457
In diesem Fall werden die 6 Primzahlen 2, 5, 13, 229, 457 und 1201 verwendet.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |