[zurück]

5. Die Eulersche Zahl e

 [vor]

Die Eulersche Zahl e [22, 23, 24, 25] lautet.

e = 2,718281828459045235360287471352662497757247093699959574966967627724077

Sie läßt sich leicht durch eine Reihenentwicklung berechnen

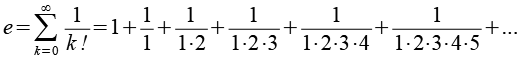
Die Reihe konvergiert recht schnell, fehlerhafte Stellen sind rot markiert.

k = 5 2,716666666666666666666666666666666666666666666666666666666666
k = 10 2,718281801146384479717813051146384479717813051146384479717813
k = 15 2,718281828458994464285469576474867480158485449490740496031501
k = 20 2,718281828459045235339784490666415886146403434540261720776551
k = 30 2,718281828459045235360287471352662372225702130983481815815378
k = 40 2,718281828459045235360287471352662497757247093699928953181184
k = 50 2,718281828459045235360287471352662497757247093699959574966967

Für den Kehrwert gilt.

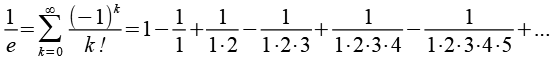
Die Eulersche Zahl e läßt sich auch über einen Grenzwert berechnen.

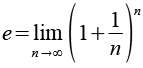
n = 1010 2,7182818283231311439497940012972294998851799338840
n = 1020 2,7182818284590452353466960622103672715805702442603
n = 1030 2,7182818284590452353602874713513033568430175710823
n = 1040 2,7182818284590452353602874713526624977571111796085
n = 1050 2,7182818284590452353602874713526624977572470936999

Berechnung nach der catalansche Darstellung.

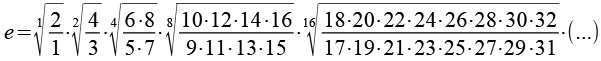
2,0000000
2,3094010
2,4991519
2,6047292
2,6604675
2,6891099
2,7036290
2,7109386
2,7146060
2,7164428
2,7173620
2,7178218
2,7180518
2,7181668
2,7182243
2,7182530
2,7182674
2,7182746
2,7182782
2,7182800

Die Berechgnung konvergiert sehr schlecht und führt sehr schnell zu sehr großen Zahlen, z.B.


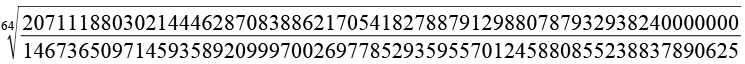
Von der Zahl e leitet sich auch die Eulerschen Identität ab, sie gilt auch als schönste Gleichung, da sie die Eulersche Zahl e, die Kreiszahl pi, die imaginäre Einheit i, die reelle Einheit 1 und die Null miteinander verbindet.

        bzw.         

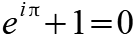
Die Eulersche Identität läßt sich wie folgt herleiten. Fangen wir zuerst mit der Funktion ex an, sie läßt sich als Reihenentwicklung darstellen.

Für eix gilt entsrechend.

Da i2 = -1 gilt läßt sich die Gleichung vereinfachen.

Jetzt sortieren wir die Reihenentwicklung nach Gliedern mit i und klammern i aus..

Das entsricht den Reihenentwicklungen für die Funktionen sin(x) und cos(x).

Dadurch lassen sich die Reihenentwicklungen von eix durch die Funktionen sin(x) und cos(x) ersetzen und wir erhalten die Eulersche Formel.

Jetzt ersetzen wir x durch pi und erhalten.

Damit haben wir die Eulersche Identität hergeleitet.

[zurück] [Inhaltsverzeichnis] [vor]