| [zurück] | 4. Fibonacci Zahlen |
[vor] |
Die Fibonacci Zahlen fn werden nach folgender Formel bzw. Gesetzmäßigkeit berechnet. Die Summe zweier aufeinanderfolgender Zahlen ist dann die nächste Fibonacci Zahl.
![]()
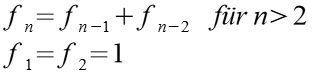
| n | fn | n | fn | |
| 1 | 1 | 11 | 89 | |
| 2 | 1 | 12 | 144 | |
| 3 | 2 | 13 | 233 | |
| 4 | 3 | 14 | 377 | |
| 5 | 5 | 15 | 610 | |
| 6 | 8 | 16 | 987 | |
| 7 | 13 | 17 | 1597 | |
| 8 | 21 | 18 | 2584 | |
| 9 | 34 | 19 | 4181 | |
| 10 | 55 | 20 | 6765 |
Die Fibonacci Zahlen können auch nach der Formel von Moivre-Binet berechnet werden.
![]()
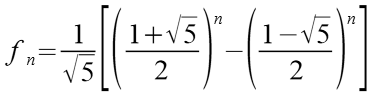
Probieren wir das für n = 13 einmal aus.
![]()

![]()
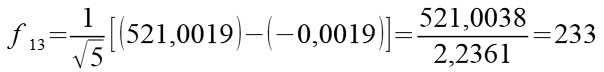
Die Fibonacci Zahlen haben faszinierende Eigenschaften, einige möchte ich hier erläutern.
Aus den Fibonacci Zahlen läßt sich der goldene Schnitt ableiten. Dazu bilden wir den Quotienten zweier benachbarter Zahlen. Je größer die Zahlen desto genauer ist das Ergebnis.
![]()
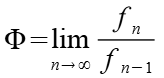
| fn | fn-1 | fn/fn-1 |
| 3 | 2 | 1,5000 |
| 5 | 3 | 1,6667 |
| 8 | 5 | 1,6000 |
| 13 | 8 | 1,6250 |
| 21 | 13 | 1,6154 |
| 34 | 21 | 1,6190 |
| 55 | 34 | 1,6176 |
| 89 | 55 | 1,6182 |
| 144 | 89 | 1,6180 |
| 233 | 144 | 1,6181 |
| 377 | 233 | 1,6180 |
Die Summe der Fibonacci Zahlen läßt sich nach folgender Formel berechnen.
![]()
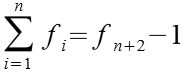
Ein Beispiel für n=10.
![]()
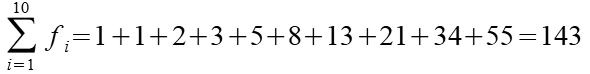
![]()
![]()
Die Summe der Quadrate der Fibonacci Zahlen läßt sich nach folgender Formel berechnen.
![]()
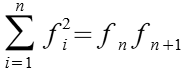
Ein Beispiel für n=8.
![]()
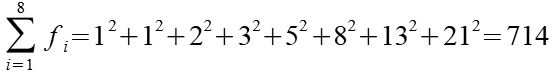
![]()
![]()
Der Quotient zweier benachbarter Fibonacci Zahlen läßt sich durch einen Kettenbruch darstellen.
![]()
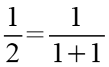
![]()
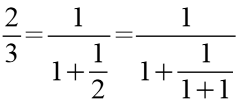
![]()

![]()
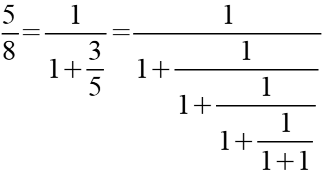
![]()

Der Bruch 10/89 läßt sich durch Fibonacci Zahlen darstellen.
![]()
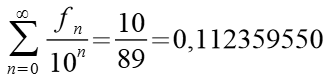
![]()
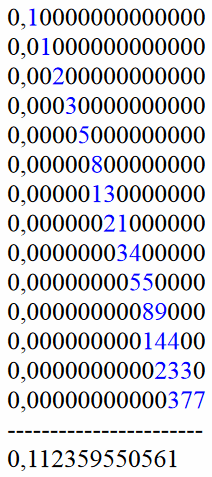
Oder auch
![]()
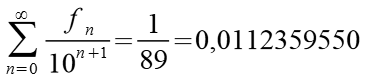
Wenn man aus der Reihe der Fibonacci Zahlen 10 aufeinander folgende Zahlen addiert so läßt sich die Summe auch aus der 7. Zahl der Reihe berechnen wenn man sie mit 11 multipliziert.
![]()
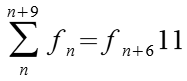
![]()
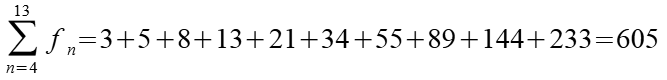
![]()
![]()
![]()
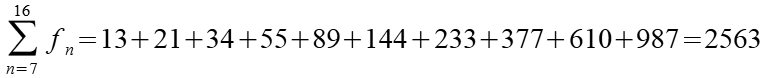
![]()
![]()
Das Quadrat einer Fibonacci Zahl läßt sich aus dem Vorgänger und dem Nachfolger der Zahl berechnen.
![]()
![]()
![]()
![]()
![]()
![]()
| [zurück] | [Inhaltsverzeichnis] | [vor] |