[zurück]

2. Der goldene Schnitt

[vor]

Ein paar Anmerkungen zum goldenen Schnitt [12, 13, 14]. Auf die Herleitung verzichte ich, der goldene Schnitt ist wie folgt definierert.

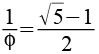
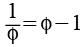
Der Goldene Schnitt ist auch eine Lösung der quadratischen Gleichung

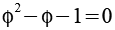
Für ein anderes Projekt hatte ich Varianten vom Goldenen Schnitt berechnet.

n mal Phi

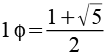	1,6180
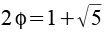	3,2361
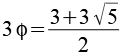	4,8541
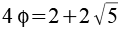	6,4721
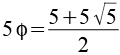	8,0902
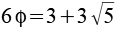	9,7082
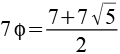	11,3262
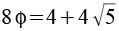	12,9443
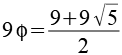	14,5623
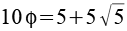	16,1803

Potenzen von Phi

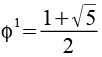	1,6180
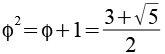	2,6180
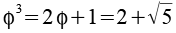	4,2361
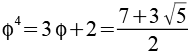	6,8541
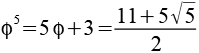	11,0902
	17,9443
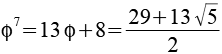	29,0344
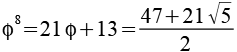	46,9787
	76,0132
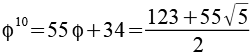	122,9919

Für die Potenzen von Phi gilt auch folgende allgemeine Formel, f_n ist eine Fibonacci Zahl.

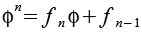
Kehrwerte der Potenzen von Phi

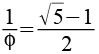	0,6180
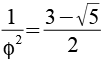	0,3820
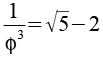	0,2361
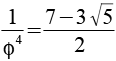	0,1459
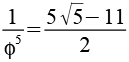	0,090170
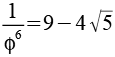	0,055728
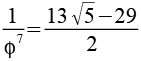	0,034442
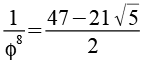	0,021286
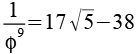	0,013156
	0,008131

Wenn man eine Potenz von Phi und deren Kehrwert alternierend addiert bzw. subtrahiert erhält man eine Folge ganzer Zahlen.

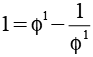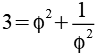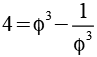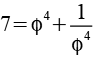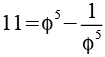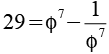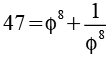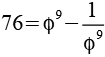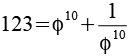Es handelt sich um eine Lukas Folge (2 1 3 4 7 11 18 29 47 76 123 199 322 521) mit L₀=2 und L₁=1. Allgemein gilt.

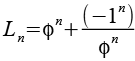       bzw.      

Dabei handelt es sich aber nur um eine andere Schreibweise der Binet Formel [21].

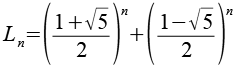
[zurück]

[Inhaltsverzeichnis]

[vor]