1. Sinus und Cosinus verschiedener Winkel
|
[zurück] | 1. Sinus und Cosinus verschiedener Winkel |
[vor] | |
Mit den Sinus- und Cosinuswerten verschiedener Winkel hatte ich mich schon in einem früheren Projekt beschäftigt. In der folgenden Tabelle habe ich alle Werte zwischen 0° und 360° mit einer Schrittweite von 3° zusammengefasst [1, 2, 3, 4, 5].
Sinus
| sin(0°) |  |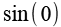
0,0000 |  |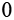
| sin(3°) |  |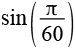
0,0523 |  |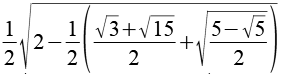
| sin(6°) |  |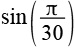
0,1045 |  |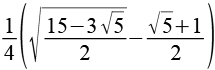
| sin(9°) |  |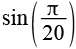
0,1564 |  |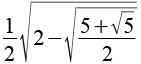
Die komplette Tabelle ist als Sinus.pdf verfügbar.
Für einzelne Winkel gibt es je nach Herleitung sehr unterschiedliche Schreibweisen, z.B für sin(3°).
| sin(3°) | |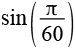
0,0523 | |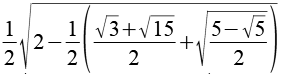
| sin(3°) | |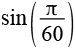
0,0523 |  |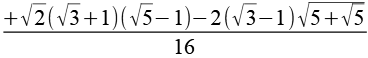
Wenn man die Vorzeichen in der Formel variiert erhält man weitere Sinuswerte ganzzahliger Winkel. Negantive Sinuswerte wurden dabei nicht berücksichtigt.
| sin(3°) | |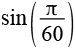
0,0523 | |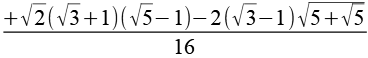
| sin(21°) |  |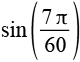
0,3584 |  |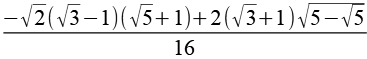
| sin(33°) |  |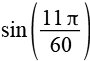
0,5446 |  |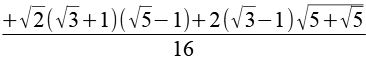
| sin(39°) |  |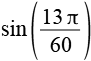
0,6293 |  |
| sin(51°) |  |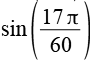
0,7771 |  |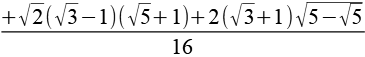
| sin(57°) |  |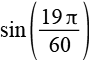
0,8387 |  |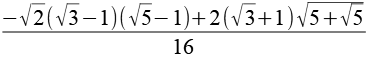
| sin(69°) |  |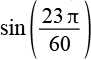
0,9336 |  |
| sin(87°) |  |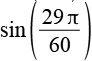
0,9986 |  |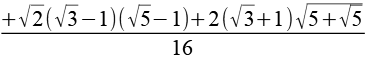
Wenn man sich die Faktoren von pi in diesen Formels ansieht (7, 11, 13, 17, 19, 23, 29) stellt man verblüffend fest das es sich um Primzahlen handelt. Die Formeln lassen sich alle auf das bekannte Additionstheorem zurückführen, z.B. für sin(33°).
Eine weitere Formel, hier führt jede Kombination der Vorzeichen zu einem Sinuswert mit ganzzahligem Winkel.
| sin(9°) | |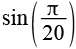
0,1564 | |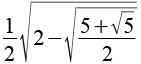
| sin(27°) |  |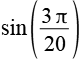
0,4540 |  |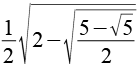
| sin(63°) |  |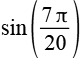
0,8910 |  |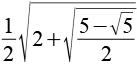
| sin(81°) |  |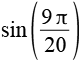
0,9877 |  |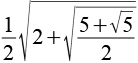
Eine weitere Formel, hier führen nur 4 Kombinationen der Vorzeichen zu einem Sinuswert mit ganzzahligem Winkel.
| sin(6°) | |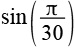
0,1045 | |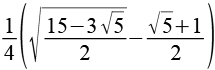
| sin(42°) |  |
0,6691 |  |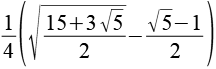
| sin(66°) |  |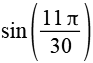
0,9135 |  |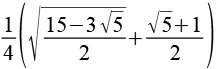
| sin(78°) |  |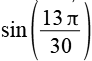
0,9781 |  |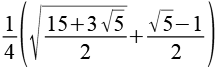
Cosinus
| cos(0°) |  |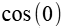
1,0000 |  |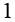
| cos(3°) |  |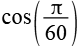
0,9986 |  |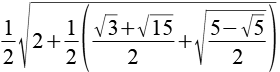
| cos(6°) |  |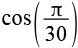
0,9945 |  |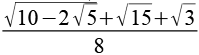
| cos(9°) |  |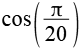
0,9877 |  |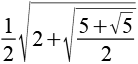
Die komplette Tabelle ist als Cosinus.pdf verfügbar.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |