7.4. Großes Ikosaeder
|
[zurück] | 7.4. Großes Ikosaeder |
[vor] | |
Das Große Ikosaeder leitet sich vom Ikosaeder ab, dessen 12 Ecken werden zu 20 sich schneidenden gleichseitigen Dreiecken verbunden.
 |
 |
| Isometrie | Dimetrie |
| Name | Großes Ikosaeder Great icosahedron |
| Anzahl Ecken | 12 |
| Anzahl Flächen | 20 gleichseitige Dreiecke |
Die einzelnen Dreiecke wurden unterschiedlich eingefärbt.
Die Dreiecke bilden Pentagramme.
Das Große Ikosaeder mit seiner Umkugel.
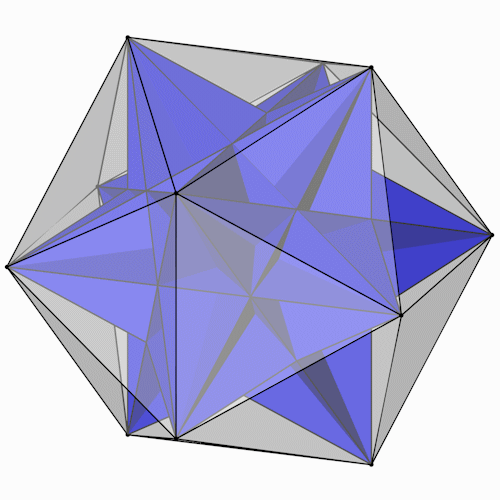
Das Große Ikosaeder mit dem Ikosaeder als Hüllkörper.
Die Koordinaten der Eckpunkte des Großen Ikosaeders sind identisch mit denen des Ikosaeders. Sie lassen sich aus folgender Beziehung herleiten. Phi ist der goldene Schnitt.
Daraus werden die geraden Permutationen gebildet.
Durch Variation der Vorzeichen entstehen die 12 Punkte.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |